Voici un distrayant problème posé sur l’excellent blogue Futility Closet.
An ant will always position itself so that it’s precisely twice as far from vinegar as from honey. If we put a dab of vinegar at A and a dab of honey at B and we release a troop of ants, what formation will they take up ?
On peut aborder le problème de manière encore plus générale. Quel est le lieu de points \(P\) tel que le rapport des distances entre le point \(P\) et les points \(A\) et \(B\) soit constant ? En d’autres mots, on cherche le lieu de points \(P\) tel que\[\frac{m\overline{PA}}{m\overline{PB}}\ = \ k\]ou de la même manière\[m\overline{PA}\ = \ k\cdot m\overline{PB}\]avec \(A\) et \(B\) donnés. La solution est triviale si \(k=1\) puisque le lieu de points est tout simplement la médiatrice de \(AB\). Si \(k\neq 1\), cependant, la solution est diablement moins évidente. Voyons. On peut toujours trouver un point \(C\) sur \(\overline{AB}\) qui satisfasse ladite condition.
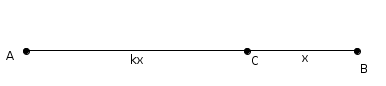 Ici,\[m\overline{CA}\ = \ k\cdot m\overline{CB}\]On considère ensuite un point \(D\) hors de \(\overline{AB}\)
Ici,\[m\overline{CA}\ = \ k\cdot m\overline{CB}\]On considère ensuite un point \(D\) hors de \(\overline{AB}\)
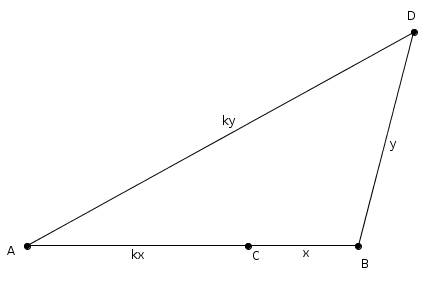 qui satisfasse la même condition.\[m\overline{DA}\ = \ k\cdot \overline{DB}\]Le théorème de la bissectrice nous indique que la bissectrice (ici, intérieure) de l’angle \(D\) partage le côté opposé dans le rapport des côtés de l’angle. Or, c’est exactement ce qu’on a ici, si bien que la bissectrice (intérieure) de l’angle \(D\) passe par \(C\).
qui satisfasse la même condition.\[m\overline{DA}\ = \ k\cdot \overline{DB}\]Le théorème de la bissectrice nous indique que la bissectrice (ici, intérieure) de l’angle \(D\) partage le côté opposé dans le rapport des côtés de l’angle. Or, c’est exactement ce qu’on a ici, si bien que la bissectrice (intérieure) de l’angle \(D\) passe par \(C\).
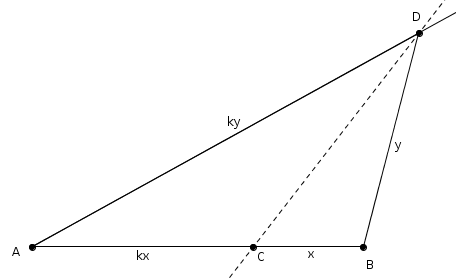 Or, la bissectrice extérieure possède les mêmes propriétés.
Or, la bissectrice extérieure possède les mêmes propriétés.
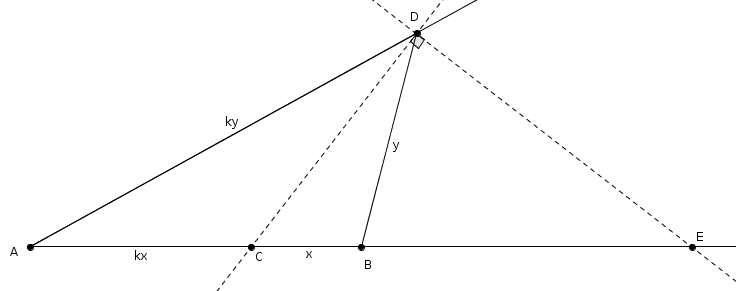
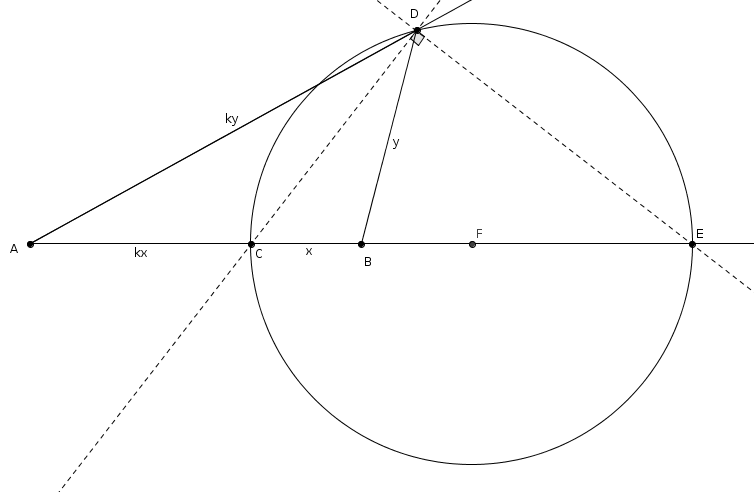
Cela nous permet de trouver un autre point \(E\) qui satisfasse la condition. Les points \(C\) et \(E\), sur la droite \(AB\) (on dit que \(A\), \(B\), \(C\) et \(E\) sont colinéaires), tels que\[m\overline{CA} \ = \ k\cdot m\overline{CB}\]et \[m\overline{EA} \ = \ k\cdot m\overline{EB}\]sont fixes : ils ne sont déterminés que par \(A\), \(B\) (fixes) et le rapport \(k\). Leur position ne dépend pas de celle de \(D\) ! Et comme l’angle \(CDE\) est droit, le lieu décrit par \(D\) est donc un cercle de diamètre \(\overline{CE}\).
Appolonius de Perga est celui qui a proposé le premier cette définition alternative du cercle comme lieu de points.