La somme des inverses des nombres triangulaires
\[S = 1 + \frac{1}{3} + \frac{1}{6} + \frac{1}{10}+\frac{1}{15} + \frac{1}{21} + \ \dots\]En 1672, Gottfried Wilhem Leibniz est un diplomate allemand en poste à Paris et l’atmosphère intellectuelle de l’époque lui sied bien. C’est à ce moment qu’il admettrait lui-même qu’il estime sa formation mathématique déficiente, formation qui se résume à l’étude des œuvres classiques. Par chance, il rencontre à Paris le Danois Christiaan Huygens, dont la liste des réalisations mathématiques et scientifiques est déjà longue. Huygens, pas exactement à titre de professeur mais plutôt à titre de mentor, guide le jeune Leibniz dans ses découvertes mathématiques. Huygens lui soumet ce problème : « Quelle est la somme des inverses des nombres triangulaires ? » En d’autres mots, il lui faut déterminer la valeur de \(S\) dans \[S = 1 + \frac{1}{3} + \frac{1}{6} + \frac{1}{10}+\frac{1}{15} + \frac{1}{21} + \ \dots\]et où les nombres triangulaires sont les nombres de la forme \[T_{k} = \frac{k(k+1)}{2}\]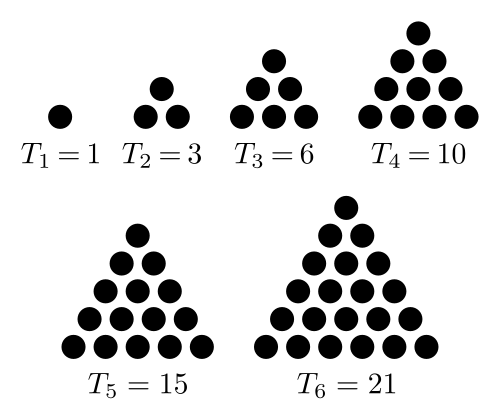
Les premiers nombres triangulaires [0]
Leibniz commence par multiplier la somme par \(\frac{1}{2}\) et obtient \[\frac{1}{2}S = \frac{1}{2}+\frac{1}{6} + \frac{1}{12} + \frac{1}{20} + \frac{1}{30} + \ \dots\]Il remplace ensuite \(\frac{1}{2}\) par \(1-\frac{1}{2}\), \(\frac{1}{6}\) par \(\frac{1}{2}-\frac{1}{3}\), \(\frac{1}{12}\) par \(\frac{1}{3}-\frac{1}{4}\) et ainsi de suite. \[\frac{1}{2}S = \left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+\left(\frac{1}{4}-\frac{1}{5}\right) + \ \dots \]Il lui suffit ensuite de se débarrasser des parenthèses afin d’obtenir \[\frac{1}{2}S = 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\ \dots \]et de simplifier toutes les fractions deux à deux pour obtenir \[\frac{1}{2}S = 1\]ce qui lui donne en multipliant par \(2\) \[S = 2\]la solution au problème de Huygens. Ce résultat, bien que peu convaincant de par les standards actuels de rigueur, laisse néanmoins présager chez Leibniz une extraordinaire perspicacité mathématique. Lorsqu’il quitte Paris en 1676 (seulement quatre ans plus tard!) il a déjà ébauché les principes fondamentaux du calcul différentiel et intégral.
La somme des inverses des nombres carrés
\[S = 1 + \frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \ \dots \ \]Saut dans le temps de deux décennies : entrent en scène les colorés frères Jakub et Johann Bernoulli, mathématiciens doués et fidèles successeurs de Leibniz. En 1689, Jakub publie son Tractatus de seriebus infinitus, traité sur les séries infinies comportant, entre autres, la preuve de la divergence de la série harmonique de son frère Johann (les preuves de Nicole Oresme et du mathématicien italien Pietro Mengoli leur étant vraisemblablement inconnues). C’est dans ce traité que Jakub s’attaque à la somme des inverses des carrés.\[S = 1 + \frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \ \dots \ \]Il remarque que \(\frac{1}{4}<\frac{1}{3}\), que \(\frac{1}{9}<\frac{1}{6}\), que \(\frac{1}{16}<\frac{1}{10}\) et qu’en général pour \(k>1\), \[\frac{1}{k^{2}}<\frac{1}{\frac{k(k+1)}{2}}\]Il s’applique donc à écrire \[1 + \frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \ \dots \ + \frac{1}{k^{2}} + \ \dots \ < 1 + \frac{1}{3} + \frac{1}{6} + \frac{1}{10} + \ \dots \ + \frac{1}{\frac{k(k+1)}{2}} + \ \dots \ = 2\]Avec sa règle de comparaison, Jakub trouve que la séries des inverses des carrés converge vers un nombre plus petit que \(2\). Cependant, malgré tout leur brio, et surtout malgré toute leur arrogance et leur orgueil, les Bernoulli sont incapables de trouver la valeur exacte de cette somme. Depuis sa ville natale, Bâle, en Suisse, Jakub écrit à toute l’intelligentsia européenne et demande de l’aide là où il a échoué. Pour que l’appel du « problème de Bâle » trouve écho, il faut attendre 45 ans et un talent mathématique inégalé, élève de Johann Bernouilli lui-même : l’incomparable Leonhard Euler. C’est en 1734 qu’il détermine (pour une première fois) la valeur de cette somme et il s’agit de l’un de ses premiers triomphes qui cautionne son statut de génie mathématique à travers toute l’Europe.

Euler utilise dans sa preuve deux résultats préliminaires. Le premier résultat est la série de Taylor de la fonction sinus \[\sin(x) = x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}+\frac{x^{9}}{9!}-\ \dots \]Le deuxième concerne l’écriture d’un polynôme (fini) sous sa forme factorisée. On considère un polynôme \(p\) de degré \(n\) possédant \(n\) racines \[a_{0}, a_{1}, a_{2}, a_{3}, a_{4}, \ \dots \ , a_{n}\]et pour lequel on a \[p(0) = 1\]Il est alors possible d’écrire le polynôme p sous cette forme \[p(x) = \left(1-\frac{x}{a_{0}}\right)\left(1-\frac{x}{a_{2}}\right)\left(1-\frac{x}{a_{3}}\right)\left(1-\frac{x}{a_{4}}\right) \ \dots \ \left(1-\frac{x}{a_{n}}\right)\]En substituant \(x\) par les valeurs \(0\), \(a_{0}\), \(a_{1}\), \(a_{2}\), … , \(a_{n}\), il est facile de voir que d’une part \[p(0)=1\]et d’autre part \[p(a_{0})=p(a_{1})=p(a_{2})=p(a_{3}) = \ \dots \ = p(a_{n}) = 0\]Euler considère la fonction \[f(x)=1-\frac{x^{2}}{3!}+\frac{x^{4}}{5!}-\frac{x^{6}}{7!}+\frac{x^{8}}{9!}-\ \dots \]Pour lui, il ne s’agit que d’un polynôme infini pour lequel \[f(0) = 1\]Pour \(x\neq 0\), il réécrit le polynôme comme \begin{align*}f(x) &= \frac{x\left(1-\frac{x^{2}}{3!}+\frac{x^{4}}{5!}-\frac{x^{6}}{7!}+\frac{x^{8}}{9!}-\ \dots \right)}{x} \\ \\ &=\frac{x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}+\frac{x^{9}}{9!}-\ \dots}{x}\end{align*}l’expression au numérateur étant la série du sinus. Il réécrit donc le tout comme \[f(x) =\frac{\sin(x)}{x}\]toujours avec \(x\neq 0\). Il s’intéresse ensuite aux racines de la fonction \[f(x) = 0\]ce qui revient à résoudre en multipliant par \(x\) de chaque côté \[\sin(x) = 0\]On sait que les racines de la fonction sinus sont \[0, \pm\pi, \pm 2\pi, \pm 3\pi, \ \dots\]et donc avec la restriction sur le domaine, les racines de la fonction \(f\) sont \[\pm \pi, \pm 2\pi, \pm 3\pi, \ \dots\]Euler, avec, d’une part, l’extraordinaire clairvoyance qu’on lui connait et, d’autre part, la rigueur beaucoup plus souple de l’époque, étend ce qu’il sait être vrai pour les polynômes finis aux polynômes infinis. Il factorise la fonction \(f\) de telle manière \[f(x) = \left(1-\frac{x}{\pi}\right)\left(1-\frac{x}{-\pi}\right)\left(1-\frac{x}{2\pi}\right)\left(1-\frac{x}{-2\pi}\right)\left(1-\frac{x}{3\pi}\right)\left(1-\frac{x}{-3\pi}\right) \ \dots\]Il regroupe ensuite les facteurs deux par deux \[f(x) = \left(\left(1-\frac{x}{\pi}\right)\left(1-\frac{x}{-\pi}\right)\right)\left(\left(1-\frac{x}{2\pi}\right)\left(1-\frac{x}{-2\pi}\right)\right)\left(\left(1-\frac{x}{3\pi}\right)\left(1-\frac{x}{-3\pi}\right)\right) \ \dots\]ces facteurs étant des différences de carrés \[f(x) = \left(1-\frac{x^{2}}{\pi^{2}}\right)\left(1-\frac{x^{2}}{4\pi^{2}}\right)\left(1-\frac{x^{2}}{9\pi^{2}}\right)\left(1-\frac{x^{2}}{16\pi^{2}}\right) \ \dots\]ce qui nous mène à cette égalité particulièrement formidable \[1-\frac{x^{2}}{3!}+\frac{x^{4}}{5!}-\frac{x^{6}}{7!}+\frac{x^{8}}{9!}-\ \dots = \left(1-\frac{x^{2}}{\pi^{2}}\right)\left(1-\frac{x^{2}}{4\pi^{2}}\right)\left(1-\frac{x^{2}}{9\pi^{2}}\right)\left(1-\frac{x^{2}}{16\pi^{2}}\right) \ \dots\]et typiquement eulérienne : une somme infinie à gauche et un produit infini à droite. À ce moment, Euler fait preuve d’encore plus d’audace et sort un autre tour de son sac : il s’imagine multiplier le produit infini à droite et regrouper les termes semblables. Le premier terme serait le produit de tous les \(1\) et c’est, bien entendu, \(1\). Pour obtenir le deuxième terme, en \(x^{2}\), il fait le produit du terme \(1\) de tous les facteurs sauf un et du terme en \(x^{2}\) de ce facteur. La multiplication infinie d’Euler lui donne quelque chose comme \[1-\frac{x^{2}}{3!}+\frac{x^{4}}{5!}-\frac{x^{6}}{7!}+ \ \dots \ = 1-\left(\frac{1}{\pi^{2}}+\frac{1}{4\pi^{2}}+\frac{1}{9\pi^{2}}+\frac{1}{16\pi^{2}}+ \ \dots \ \right)x^{2}+\left(\dots\right)x^{4}- \ \dots \]Dans le cas qui l’intéresse, les coefficients des termes de degrés supérieurs à \(2\) dans le membre de droite de l’égalité lui sont inconnus et de toute façon inutiles. Maintenant qu’il possède une égalité de deux sommes infinies, il égale les coefficients des termes en \(x^{2}\) \[-\frac{1}{3!}=-\left(\frac{1}{\pi^{2}}+\frac{1}{4\pi^{2}}+\frac{1}{9\pi^{2}}+\frac{1}{16\pi^{2}} + \ \dots \right)\]En multipliant par \(-1\) de chaque côté et en observant que \(3! = 6\), il a d’abord \[\frac{1}{6} = \frac{1}{\pi^{2}}+\frac{1}{4\pi^{2}}+\frac{1}{9\pi^{2}}+\frac{1}{16\pi^{2}} + \ \dots\]puis en multipliant chaque côté par \(\pi^{2}\), il obtient le résultat si remarquable \[1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25} + \ \dots \ = \frac{\pi^{2}}{6}\]qui résistait à l’assaut des mathématiciens depuis des décennies. Un nombre de prime abord invraisemblable mais définitivement plus petit que \(2\) tel que prédit par Jakub. Une égalité dans laquelle on retrouve, d’un côté, les nombres carrés et de l’autre, la constante du cercle.
En reprenant ceci \[\frac{\sin(x)}{x}=\left(1-\frac{x^{2}}{\pi^{2}}\right)\left(1-\frac{x^{2}}{4\pi^{2}}\right)\left(1-\frac{x^{2}}{9\pi^{2}}\right)\left(1-\frac{x^{2}}{16\pi^{2}}\right) \ \dots\]Euler substitue \[x = \frac{\pi}{2}\]et obtient\[\frac{\sin\left(\frac{\pi}{2}\right)}{\frac{\pi}{2}}=\left(1-\frac{\left(\frac{\pi}{2}\right)^{2}}{\pi^{2}}\right)\left(1-\frac{\left(\frac{\pi}{2}\right)^{2}}{4\pi^{2}}\right)\left(1-\frac{\left(\frac{\pi}{2}\right)^{2}}{9\pi^{2}}\right)\left(1-\frac{\left(\frac{\pi}{2}\right)^{2}}{16\pi^{2}}\right) \ \dots\] La fonction sinus atteignant son maximum de \(1\) à cette valeur, il obtient \[\frac{1}{\frac{\pi}{2}}= \left(1-\frac{1}{4}\right)\left(1-\frac{1}{16}\right)\left(1-\frac{1}{36}\right)\left(1-\frac{1}{64}\right) \ \dots\]Il effectue ensuite les soustractions dans chaque parenthèse et obtient \[\frac{2}{\pi}=\left(\frac{3}{4}\right)\left(\frac{15}{16}\right)\left(\frac{35}{36}\right)\left(\frac{63}{64}\right) \ \dots\]ou en inversant \[\frac{\pi}{2} = \left(\frac{4}{3}\right)\left(\frac{16}{15}\right)\left(\frac{36}{35}\right)\left(\frac{64}{63}\right)\]Enfin en factorisant les numérateurs et dénominateurs, il trouve \[\frac{\pi}{2} = \left(\frac{2\times 2}{1\times 3}\right)\left(\frac{4\times 4}{3 \times 5}\right)\left(\frac{6 \times 6}{5 \times 7}\right)\left(\frac{8\times 8}{7 \times 9}\right) \ \dots\]la formule du mathématicien anglais John Wallis, qui exprime \(\frac{\pi}{2}\) comme le quotient du produit des nombres pairs au numérateur et des nombres impairs au dénominateur (chaque nombre pair et chaque nombre impair étant là deux fois dans le produit)\[\frac{\pi}{2} = \frac{2\times 2 \times 4 \times 4 \times 6 \times 6 \times 8 \times 8 \times \ \dots}{1 \times 3 \times 3 \times 5 \times 5 \times 7 \times 7 \times 9 \times \ \dots}\]Lorsque Johann apprend qu’Euler a trouvé la solution au problème de Bâle, il écrit : Utinam Frater superstes esset ! (si seulement mon frère était encore en vie !) Cependant la preuve ne fait pas l’unanimité et bien qu’on accepte la solution, quelques détracteurs, dont notamment le fils de Johann, Daniel, expriment à Euler leur réserve quant à la démarche menant à ladite solution. Euler répond à ses détracteurs avec une preuve complètement différente mais tout aussi ingénieuse se basant sur trois lemmes et faisant usage sans réserve du calcul intégral.
La somme des inverses des carrés (bis)
Il existe aujourd’hui des dizaines d’autres preuves de ce résultat (voir [1]). Voici non pas la deuxième preuve plus rigoureuse d’Euler, mais une preuve récente élémentaire (sans calcul intégral, sauf pour une toute petite limite à la toute fin). C’est sans aucun doute celle qui nécessite le moins de notions préalables (bien qu’elle soit plutôt longue). Elle semble être apparue comme exercice dans un livre des frères Akiva et Isaak Yaglom, dont l’édition originale russe est parue en 1954. D’autres versions de cette preuve ont été redécouverte par F. Holme (1970), I. Papadimitriou (1973) et Ransford (1982) qui l’attribua à John Scholes. On retrouve cette preuve dans le superbe livre Proofs from THE BOOK (4ième édition) de Aigner et Ziegler (2010).
L’idée de la preuve est de coincer la série \[\frac{1}{1^{2}}+\frac{1}{2^{2}}+\frac{1}{3^{2}}+ \ \dots \ + \frac{1}{m^{2}}\]dans une double inégalité dans laquelle les deux côtés tendent vers la même valeur, \(\dfrac{\pi^{2}}{6}\) lorsque \(m \to \infty\). On se rappelle d’abord la formule du binôme de Newton \[\left(a+b\right)^{n}=\binom{n}{0}a^{n}+\binom{n}{1}a^{n-1}b+\binom{n}{2}a^{n-2}b^{2}+\ \dots \ +\binom{n}{n-1}ab^{n-1}+\binom{n}{n}b^{n}\]En reprenant la formule d’Euler (décidément!) \[e^{ix}=\cos(x)+i\sin(x)\]et en élevant le tout à l’exposant \(n\) \begin{align*}\left(e^{ix}\right)^{n} &= e^{inx} \\ \\ &= \cos(nx) + i\sin(nx) \\ \\ &= \left(\cos(x) + i\sin(x)\right)^{n}\end{align*}il nous est possible d’appliquer la formule du binôme à droite, avec \(a = \cos(x)\) et \(b = i\sin(x)\). On obtient \begin{align*}\left(\cos(x) + i\sin(x)\right)^{n} = &\binom{n}{0}\cos^{n}+\binom{n}{1}\cos^{n-1}(x)\left(i\sin(x)\right)+\binom{n}{2}\cos^{n-2}(x)\left(i\sin(x)\right)^{2} + \\ &\binom{n}{3}\cos^{n-3}(x)\left(i\sin(x)\right)^{3}+\binom{n}{4}\cos^{n-4}(x)\left(i\sin(x)\right)^{4}+ \ \dots\end{align*}et comme \(i^{0}-1\), \(i^{1}=i\), \(i^{2}=-1\), \(i^{3}=-i\), \(i^{4} = 1\), … , on obtient \begin{align*}\left(\cos(x) + i\sin(x)\right)^{n} = &\binom{n}{0}\cos^{n}+i\binom{n}{1}\cos^{n-1}(x)\sin(x)-\binom{n}{2}\cos^{n-2}(x)\sin^{2}(x) – \\ i&\binom{n}{3}\cos^{n-3}(x)\sin^{3}(x)+\binom{n}{4}\cos^{n-4}(x)\sin^{4}(x)+ \ \dots\end{align*}En ne considérant que la partie imaginaire de cette égalité, on a \[\sin(nx) = \binom{n}{1}\cos^{n-1}(x)\sin(x)-\binom{n}{3}\cos^{n-3}(x)\sin^{3}(x)\pm \ \dots\]On divise chaque côté par \(\sin^{n}(x)\) afin d’obtenir \[\frac{\sin(nx)}{\sin^{n}(x)} = \binom{n}{1}\cot^{n-1}(x)-\binom{n}{3}\cot^{n-3}(x) \pm \ \dots \]On considère des valeurs de \(n\) impaires, et on pose \[n = 2m+1\]et donc \[\frac{\sin(nx)}{\sin^{n}(x)} = \binom{2m+1}{1}\cot^{2m}(x)-\binom{2m+1}{3}\cot^{2m-2}(x) \pm \ \dots\]et pour \(x\) on considère les \(m\) différentes valeurs \[x = \frac{r\pi}{2m+1}\]avec \[r = 1, \, 2,\, 3,\, \dots \, , \, m\]On remarque que pour chacune de ces valeurs, on a \[nx = r\pi\]et donc, toujours pour ces valeurs, \[\sin(nx) = \sin(r\pi) = 0\]Enfin, \[0<x<\frac{\pi}{2}\]implique \(m\) valeurs strictement positives pour \(\sin(x)\). Puisque pour ces \(m\) valeurs de \(x\) on a \(\sin(nx) = 0\), l’équation \[\frac{\sin(nx)}{\sin^{n}(x)} = \binom{2m+1}{1}\cot^{2m}(x)-\binom{2m+1}{3}\cot^{2m-2}(x)\pm \ \dots\]devient \[0 = \binom{2m+1}{1}\cot^{2m}(x)-\binom{2m+1}{3}\cot^{2m-2}(x)\pm \ \dots\]toujours pour ces \(m\) valeurs de \(x\). En réécrivant, on obtient \[0 = \binom{2m+1}{1}\left(\cot^{2}(x)\right)^{m}-\binom{2m+1}{3}\left(\cot^{2}(x)\right)^{m-1}\pm \ \dots\]Sur ce, on considère le polynôme \(p\) suivant \[p(t) = \binom{2m+1}{1}t^{m}-\binom{2m+1}{3}t^{m-1}\pm \ \dots \ + (-1)^{m}\binom{2m+1}{2m+1}\]On connait ses \(m\) racines distinctes ! Ce sont \[a_{r} = \cot^{2}\left(\frac{r\pi}{2m+1}\right)\]pour \[r = 1,\, 2,\, 3,\, \dots \, , \, m\]À l’instar d’Euler, on peut donc réécrire le polynôme sous sa forme factorisée \[p(t) = \binom{2m+1}{1}\left(t-\cot^{2}\left(\frac{\pi}{2m+1}\right)\right)\left(t-\cot^{2}\left(\frac{2\pi}{2m+1}\right)\right) \ \dots \ \left(t-\cot^{2}\left(\frac{m\pi}{2m+1}\right)\right)\]Remarquons que le coefficient de \(t^{m-1}\) d’un polynôme \[p(t) = c(t-a_{1})(t-a_{2}) \ \dots \ (t-a_{m})\]est \[-c\left(a_{1}+a_{2}+ \ \dots \ + a_{m}\right)\]après multiplication des facteurs [2]. On peut donc comparer les coefficients de \(t^{m-1}\) dans \[p(t) = \binom{2m+1}{1}t^{m}-\binom{2m+1}{3}t^{m-1}\pm \ \dots \ + (-1)^{m}\binom{2m+1}{2m+1}\]et \[p(t) = \binom{2m+1}{1}\left(t-\cot^{2}\left(\frac{\pi}{2m+1}\right)\right)\left(t-\cot^{2}\left(\frac{2\pi}{2m+1}\right)\right) \ \dots \ \left(t-\cot^{2}\left(\frac{m\pi}{2m+1}\right)\right)\]afin d’obtenir \[-\binom{2m+1}{3}=-\binom{2m+1}{1}(a_{1}+a_{2}+a_{3} + \ \dots \ +a_{r})\]Cela nous permet de trouver l’expression qui représente la somme des racines \[a_{1}+a_{2}+a_{3}+ \ \dots \ + a_{r} = \frac{\binom{2m+1}{3}}{\binom{2m+1}{1}}\]ce qui se simplifie comme \begin{align*}\frac{\binom{2m+1}{3}}{\binom{2m+1}{1}}&=\frac{\frac{(2m+1)!}{(2m+1-3)!(3!)}}{\frac{(2m+1)!}{(2m+1-1)!(1!)}} \\ \\ &=\frac{(2m)!}{(2m-2)!(3!)} \\ \\ &=\frac{2m(2m-1)(2m-2)!}{(2m-2)! \cdot 6} \\ \\ &=\frac{2m(2m-1)}{6}\end{align*}c’est-à-dire que \[\cot^{2}\left(\frac{\pi}{2m+1}\right)+\cot^{2}\left(\frac{2\pi}{2m+1}\right)+ \ \dots \ + \cot^{2}\left(\frac{m\pi}{2m+1}\right) = \frac{2m(2m-1)}{6}\]C’est une très jolie formule qui donne pour les premières valeurs de \(m\) \begin{align*}\cot^{2}\left(\frac{\pi}{3}\right) &= \frac{1}{3} \\ \\ \cot^{2}\left(\frac{\pi}{5}\right)+\cot^{2}\left(\frac{2\pi}{5}\right) &= 2 \\ \\ \cot^{2}\left(\frac{\pi}{7}\right) + \cot^{2}\left(\frac{2\pi}{7}\right) + \cot^{2}\left(\frac{3\pi}{7}\right) &=5 \\ \\ &\dots\end{align*}C’est aussi ce que l’on aura besoin d’un côté de la double inégalité. De l’autre, on aura besoin de \[\csc^{2}\left(\frac{\pi}{2m+1}\right) + \csc^{2}\left(\frac{2\pi}{2m+1}\right) + \ \dots \ + \csc^{2}\left(\frac{m\pi}{2m+1}\right) = \frac{2m(2m+2)}{6}\]Pour prouver cette dernière équation, on remarque que\[\cot^{2}(x) + 1 = \csc^{2}(x)\]et donc \[\cot^{2}\left(\frac{\pi}{2m+1}\right)+\cot^{2}\left(\frac{2\pi}{2m+1}\right)+ \ \dots \ +\cot^{2}\left(\frac{m\pi}{2m+1}\right)=\frac{2m(2m-1)}{6}\]devient en ajoutant \(1\) à chaque terme à gauche, donc \(m\) de chaque côté, \[\cot^{2}\left(\frac{\pi}{2m+1}\right)+1+\cot^{2}\left(\frac{2\pi}{2m+1}\right)+1+ \ \dots \ +\cot^{2}\left(\frac{m\pi}{2m+1}\right)+1=\frac{2m(2m-1)}{6}+m\]c’est-à-dire \[\csc^{2}\left(\frac{\pi}{2m+1}\right)+\csc^{2}\left(\frac{2\pi}{2m+1}\right)+ \ \dots \ + \csc^{2}\left(\frac{m\pi}{2m+1}\right)=\frac{2m(2m-1)+6m}{6}\]ou \[\csc^{2}\left(\frac{\pi}{2m+1}\right)+\csc^{2}\left(\frac{2\pi}{2m+1}\right)+ \ \dots \ + \csc^{2}\left(\frac{m\pi}{2m+1}\right)=\frac{2m(2m+2)}{6}\]On s’attaque maintenant à l’étape finale ! Puisque pour \[0<y<\frac{\pi}{2}\]on a [3] \[\sin(y)<y<\tan(y)\]cela implique que \[\frac{1}{\tan(y)}<\frac{1}{y}<\frac{1}{\sin(y)}\]ou en réécrivant\[\cot(y)<\frac{1}{y}<\csc(y)\]En élevant au carré on obtient finalement \[\cot^{2}(y)<\frac{1}{y^{2}}<\csc^{2}(y)\]Il suffit de prendre cette double inégalité et de l’appliquer à chacune des \(m\) valeurs considérées de \(x\). On somme. \[\frac{2m(2m-1)}{6}<\left(\frac{2m+1}{\pi}\right)^{2}+\left(\frac{2m+1}{2\pi}\right)^{2}+ \ \dots \ +\left(\frac{2m+1}{m\pi}\right)^{2}<\frac{2m(2m+2)}{6}\]En multipliant par \[\left(\frac{\pi}{2m+1}\right)^{2}\]partout, on obtient \[\left(\frac{\pi}{2m+1}\right)^{2}\left(\frac{2m(2m-1)}{6}\right)<\frac{1}{1^{2}}+\frac{1}{2^{2}}+\frac{1}{3^{2}}+\ \dots \ +\frac{1}{m^{2}}<\left(\frac{\pi}{2m+1}\right)^{2}\left(\frac{2m(2m+2)}{6}\right)\]Enfin, en réécrivant \[\frac{\pi^{2}}{6}\left(\frac{2m}{2m+1}\right)\left(\frac{2m-1}{2m+1}\right)<\frac{1}{1^{2}}+\frac{1}{2^{2}}+\frac{1}{3^{2}}+ \ \dots \ +\frac{1}{m^{2}}<\frac{\pi^{2}}{6}\left(\frac{2m}{2m+1}\right)\left(\frac{2m+2}{2m+1}\right)\]on s’aperçoit que la somme est coincée entre deux côtés d’une inégalité qui tendent chacun vers \[\frac{\pi^{2}}{6}\] lorsque \(m\to \infty\).
\[\phantom{S}\]
[0] https://commons.wikimedia.org/wiki/File:First_six_triangular_numbers.svg
[1] Evaluating ζ(2) Fourteen proofs compiled by Robin Chapman
[2] Par exemple, pour les premières valeurs de \(r\), on a \begin{align*}c\left(t-a_{1}\right) &= ct-ca_{1} \\ \\ c\left(t-a_{1}\right)\left(t-a_{2}\right)&=ct^{2}-c\left(a_{1}+a_{2}\right)t + ca_{1}a_{2} \\ \\ c\left(t-a_{1}\right)\left(t-a_{2}\right)\left(t-a_{3}\right)&=ct^{3}-c\left(a_{1}+a_{2}+a_{3}\right)t + c\left(a_{1}a_{2}+a_{1}a_{3}+a_{2}a_{3}\right)t-ca_{1}a_{2}a_{3} \\ \\ &\dots \end{align*}
[3] En considérant le cercle trigonométrique suivant

on a \[\text {Aire de }\triangle OAB < \text{Aire du secteur }OAB < \text{Aire de } \triangle OAC\]c’est-à-dire \[\frac{\sin(y)}{2}<\frac{y}{2}<\frac{\tan(y)}{2}\]ou tout simplement \[\sin(y)<y<\tan(y)\]
Références : William Dunham (1991), Journey Trough Genius
William Dunham (1999), Euler : The Master of Us All
Martin Aigner et Günter M. Ziegler (2004), Proofs from THE BOOK

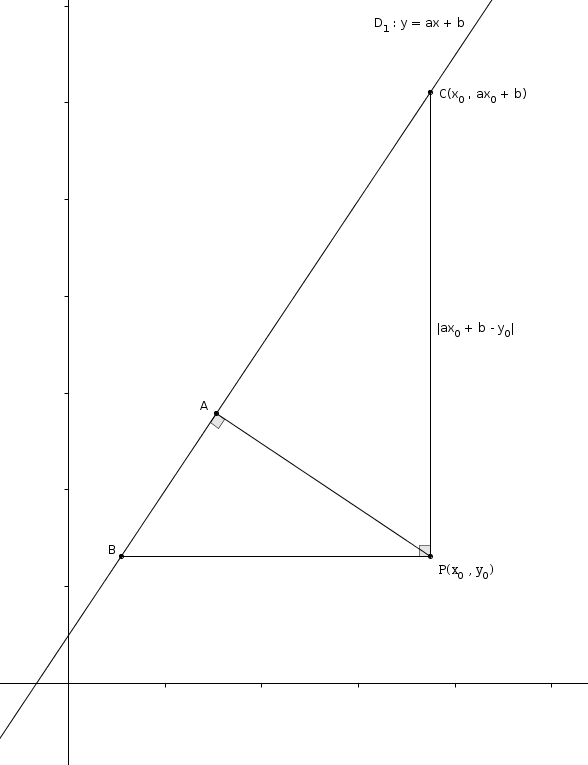 On place ensuite \(D\) sur \(BP\) à une unité de \(B\). On place \(E\) sur \(D_{1}\) de manière à former un autre triangle \(BDE\) rectangle en \(D\). Comme dans la forme fonctionnelle le coefficient \(a\) correspond à la pente de la droite, on trouve immédiatement que \(DE\) a pour mesure \(\vert a\vert\). Il s’en suit aussi qu’avec Pythagore,\[m\overline{EB}=\sqrt{1+a^{2}}\](la valeur absolue étant maintenant superflue avec le carré)
On place ensuite \(D\) sur \(BP\) à une unité de \(B\). On place \(E\) sur \(D_{1}\) de manière à former un autre triangle \(BDE\) rectangle en \(D\). Comme dans la forme fonctionnelle le coefficient \(a\) correspond à la pente de la droite, on trouve immédiatement que \(DE\) a pour mesure \(\vert a\vert\). Il s’en suit aussi qu’avec Pythagore,\[m\overline{EB}=\sqrt{1+a^{2}}\](la valeur absolue étant maintenant superflue avec le carré)