Author: The Dude

Avec deux points \(A\) et \(B\) du même côté d’une droite, on cherche un point \(C\) sur la droite qui minimise la distance \(m\overline{AC} + m\overline{CB}\). C’est le problème classique de l’homme qui part du village \(A\), s’abreuve à la rivière et termine ensuite sa course au village \(B\). Le problème, qui est de chercher ici un minimum, enligne souvent les étudiants à placer la droite et les points dans un repère cartésien et à avoir recours au calcul différentiel. Voici plutôt une preuve géométrique plus élémentaire.

On identifie \(B’\), réflexion de \(B\) par la droite. On trace ensuite \(AB’\). On prétend que l’intersection de \(AB’\) et de la droite est le point \(C\) recherché.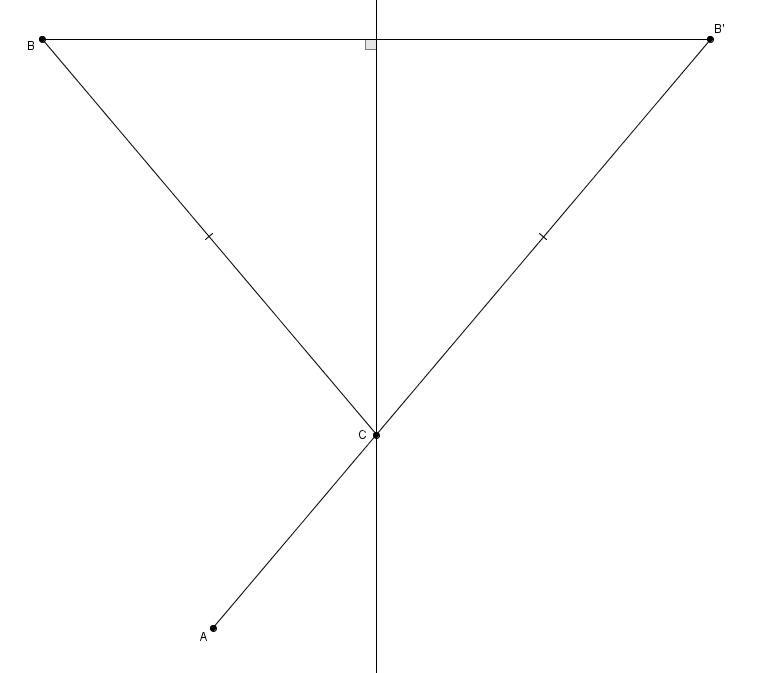En effet, on considère au contraire un autre point \(C’\), différent de \(C\), sur la droite. On trace aussi \(\overline{AC’}\) et les segments isométriques \(C’B\) et \(C’B’\) (ils sont isométriques car ce sont des côtés homologues dans des triangles isométriques). Puisque la réflexion est une isométrie, on a d’abord que \(m\overline{AC} + m\overline{CB} = m\overline{AC} + m\overline{CB’} = m\overline{AB’}\) et ensuite que \(m\overline{AC’} + m\overline{C’B} = m\overline{AC’} + m\overline{C’B’}\). En considérant le triangle \(AC’B’\), il devient apparent que \(m\overline{AC’} + m\overline{C’B’} ­> m\overline{AC} + m\overline{CB’} = m\overline{AB’}\) (dans un triangle la somme des mesures de deux côtés est toujours plus grande que la mesure du troisième).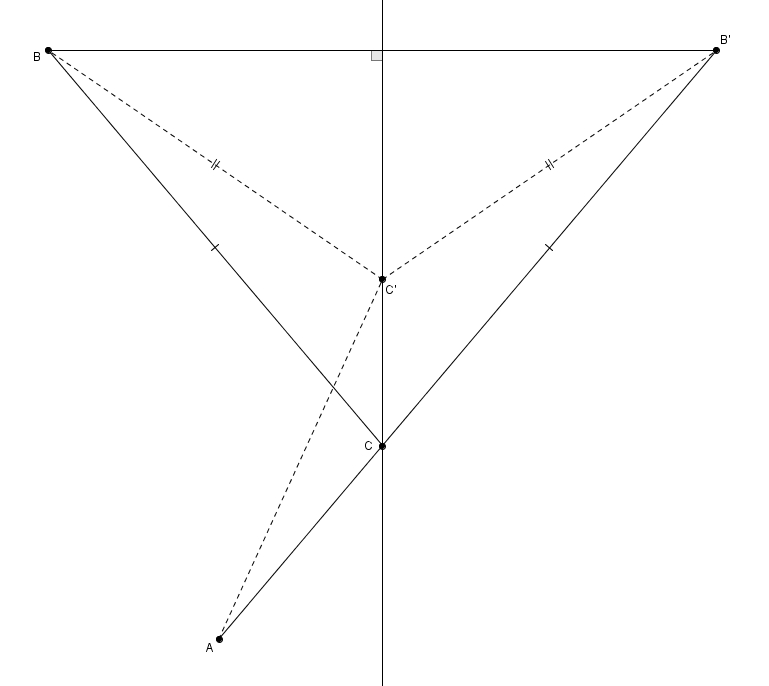Le point \(C\) tel qu’on l’a défini étant effectivement celui recherché ! En dernier lieu, on considère la figure suivante, dans laquelle on a identifié des angles.

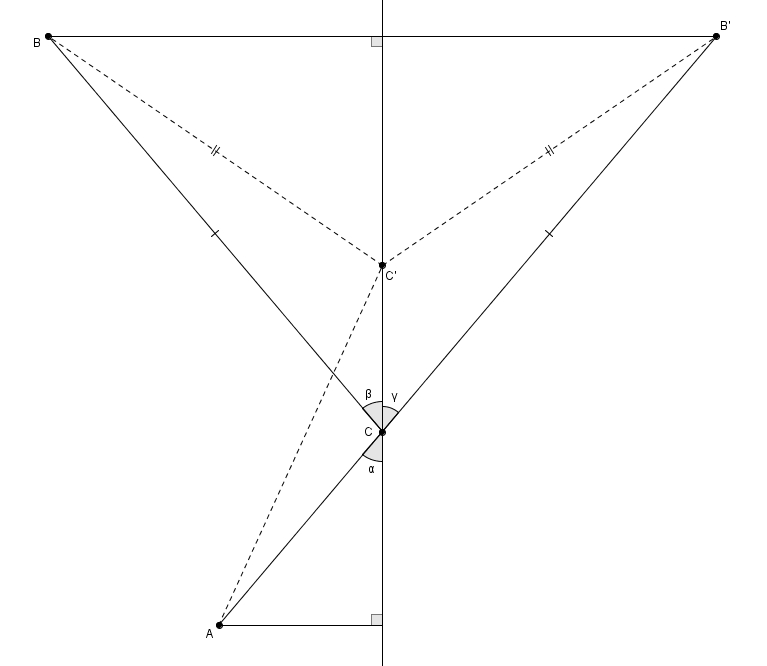Les angles \(\alpha\) et \(\gamma\) sont isométriques puisqu’ils sont opposés par le sommet. Le angles \(\beta\) et \(\gamma\) sont eux aussi isométriques puisque ce sont des angles homologues dans des triangles isométriques (qu’on peut démontrer avec le cas CAC d’isométrie). Par transitivité on trouve que les angles \(\alpha\) et \(\gamma\) sont isométriques. La solution optimale correspond donc à la situation où les segments \(AC\) et \(CB\) forment des angles isométriques avec la droite.

Ce dernier résultat nous permet d’examiner, entre autres, des propriétés de l’ellipse et de l’hyperbole.

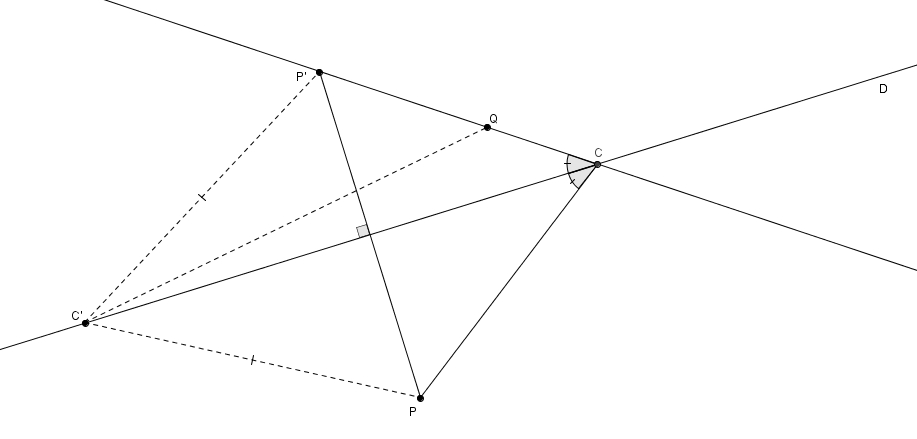
Par exemple, on considère les points \(P\) et \(Q\), du même côté de la droite \(D\), et le point \(C\) qui minimise la distance \(m\overline{PC} + m\overline{CQ}\). On sait maintenant que les segments \(PC\) et \(CQ\) forment des angles isométriques avec la droite \(D\).

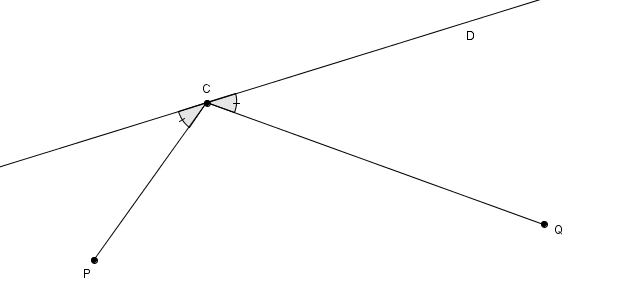Appelons \(2a\) cette distance minimale \(m\overline{PC} + m\overline{CQ}\). Le lieu de points dans le plan tel que \(m\overline{PC} + m\overline{CQ} = 2a\) est une ellipse de grand axe \(2a\) et passant par \(C\) et dont les foyers sont \(P\) et \(Q\).

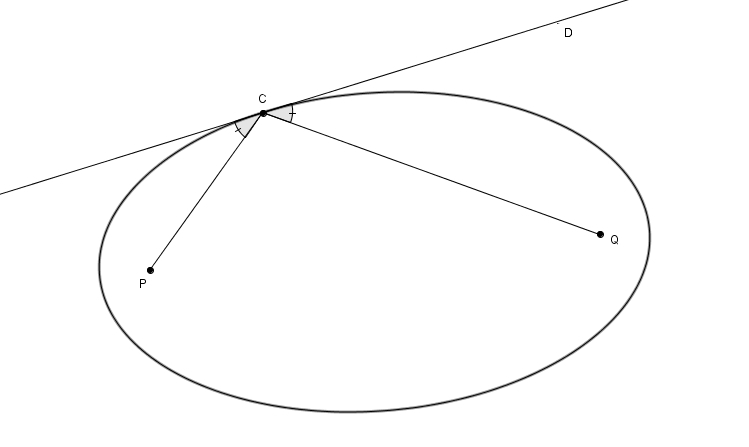La droite \(D\) n’a d’autre choix que d’être tangente à l’ellipse. Supposons le contraire et qu’elle coupe l’ellipse en \(C\) et un point autre que \(C\). Une portion de la droite est donc dans la partie intérieure de l’ellipse. Pour un point \(R\) sur cette portion de la droite à l’intérieur de l’ellipse, on a \(m\overline{PR} + m\overline{RQ} < 2a\). On obtient une contradiction ! On aurait trouvé un point \(R\) pour lequel \(m\overline{PR} + m\overline{RQ} < m\overline{PC} + m\overline{CQ}\) ce qui est bien sûr impossible puisque c’est avec \(C\) que l’on obtient la distance minimale. On vient de prouver une propriété importante de l’ellipse : les segments qui relient les foyers à un point sur l’ellipse rencontrent la tangente à l’ellipse en ce point avec le même angle.

Un raisonnement similaire nous permet d’examiner une propriété analogue dans l’hyperbole. On suppose cette fois-ci que les points \(P\) et \(Q\) ne soient pas du même côté de \(D\).

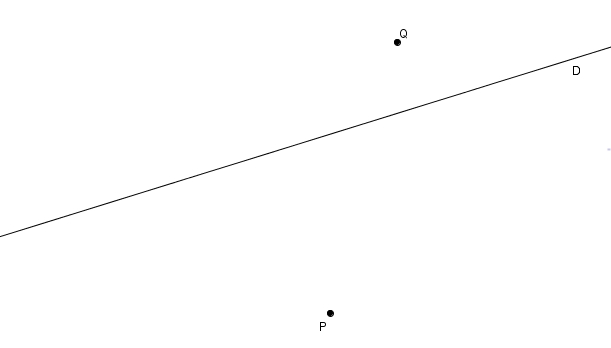On cherche à trouver le point \(C\) qui maximise \(|m\overline{PC}-m\overline{CQ}|\), c’est-à-dire la valeur absolue de la différence de \(m\overline{PC}\) et \(m\overline{CQ}\) (notons au passage que la droite \(D\) ne peut être la médiatrice de \(\overline{PQ}\) puisque dans ce cas, l’expression \(|m\overline{PC}-m\overline{CQ}|\) serait nulle partout, la médiatrice de \(\overline{PQ}\) étant le lieu de points équidistants de \(P\) et \(Q\)). Pour résoudre ce problème, on identifie \(P’\), réflexion de \(P\) par la droite \(D\). On considère un point \(C’\) quelconque sur la droite.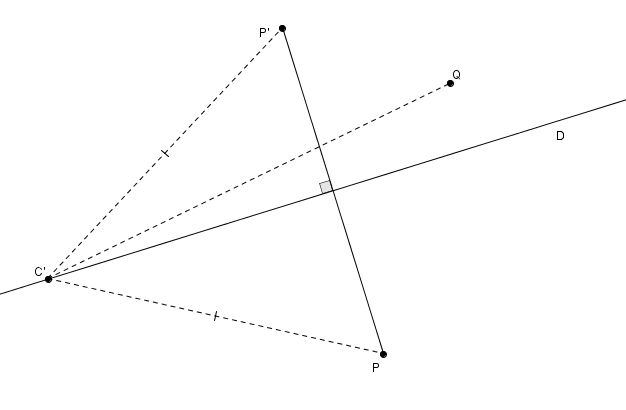Les segments \(C’P\) et \(C’P’\) sont isométriques puisque ce sont des côtés homologues dans des triangles isométriques (qu’on peut démontrer avec la cas d’isométrie CAC). On considère aussi \(\overline{C’Q}\).

Dans le triangle \(C’P’Q\), il est apparent que la quantité \(|m\overline{C’P’}-m\overline{C’Q}|\) n’est jamais plus grande que \(m\overline{P’Q}\) (la différence des mesures de deux côtés d’un triangle n’est jamais plus grande que la mesure du troisième côté). Et c’est seulement si les points \(P’\), \(Q\) et \(C’\) sont alignés sur une même droite, c’est-à-dire si \(C’\) est en \(C\) sur la figure, qu’on obtient l’égalité \(|m\overline{CP’}-m\overline{CQ}| = m\overline{P’Q}\). Comme \(CP’\) est isométrique à \(CP\), le point \(C\) correspond à la solution (le maximum recherché). Appelons \(2a\) cette différence en valeur absolue maximale \(|m\overline{CP}-m\overline{CQ}| = m\overline{P’Q}\). Le lieu de points dans le plan tel que \(|m\overline{CP}-m\overline{CQ}| = 2a\) est une hyperbole passant par \(C\) et dont les foyers sont \(P\) et \(Q\).

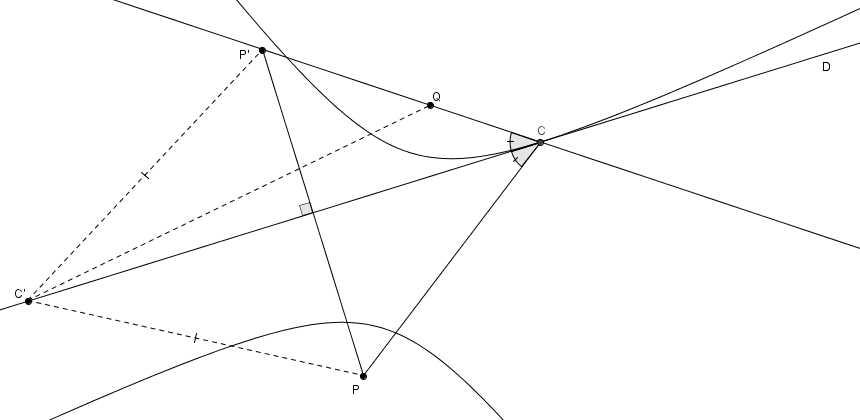Un raisonnement similaire à celui emprunté pour l’ellipse nous permet de conclure que la droite \(D\) n’a d’autre choix que d’être tangente à l’hyperbole en \(C\) puisqu’en effet, pour un point \(R\) situé entre les branches de l’hyperbole, on a \(|m\overline{RP}-m\overline{RQ}| < 2a\) et pour une point \(S\) situé de l’autre côté des branches (dans les régions qui contiennent les foyers), on a \(|m\overline{SP}-m\overline{SQ}| > 2a\).

Si \(Q\) est plus près de \(D\) que \(P\), comme c’est le cas dans notre exemple, alors la droite \(D\) touchera la branche à proximité de \(Q\) et vice-versa. Enfin, si \(P\) et \(Q\) sont à la même distance de \(D\), la droite \(D\) ne sera pas une tangente mais bien une asymptote de l’hyperbole. En effet, si \(P\) et \(Q\) sont à la même distance de \(D\), la droite \(P’Q\) sera parallèle à \(D\) et il nous sera impossible de trouver \(C\). On vient de prouver une propriété importante de l’hyperbole : les segments qui relient les foyers à un point sur l’hyperbole rencontrent la tangente à l’hyperbole en ce point avec le même angle.

Référence : R. Courant, H. Robbins et I. Stewart (1996), What is mathematics ?

On cherche les valeurs du sinus et du cosinus pour les angles suivants : \(\frac{2\pi}{5}\), \(\frac{4\pi}{5}\), \(\frac{6\pi}{5}\) et \(\frac{8\pi}{5}\).

Dans le cercle trigonométrique, ces points correspondent aux sommets d’un pentagone régulier inscrit. Dans le plan complexe, les sommets de ce pentagone inscrit dans le cercle d’équation \[z\bar{z} = 1\]correspondent aux solutions de l’équation \[z^{5}-1=0\]c’est-à-dire aux racines cinquièmes de l’unité. L’une de ces racines est évidemment \(1\). En effectuant la longue division par \(z-1\), on peut vérifier que \[(z-1)(z^{4}+z^{3}+z^{2}+z+1)=0\]ou, si \(z \neq 1\), \[z^{4} + z^{3}+z^{2}+z+1=0\]Il faut donc résoudre cette équation quartique. Mince affaire ! Heureusement, on peut ici appliquer un petit truc. Si \(z \neq 0\), on divise par \(z^{2}\) \[z^{2}+z^{1}+1+\frac{1}{z^{1}}+ \frac{1}{z^{2}}=0\]et on réarrange les termes \[z^{2}+\frac{1}{z^{2}}+z+\frac{1}{z}+1=0\]En remarquant que \[\left(z + \frac{1}{z}\right)^{2}= z^{2}+\frac{1}{z^{2}}+2\]l’équation précédente devient \begin{align*} z^{2}+\frac{1}{z^{2}}+z+\frac{1}{z}+1&=0 \\ \\ z^{2}+\frac{1}{z^{2}}+2 + z + \frac{1}{z}+1-2 &=0 \\ \\ \left(z + \frac{1}{z}\right)^{2} + \left(z + \frac{1}{z}\right)-1 &=0\end{align*}une équation du deuxième degré en \(\left(z + \frac{1}{z}\right)\) ! En utilisant la formule quadratique, on trouve que les solutions sont\[z + \frac{1}{z} = \frac{-1+\sqrt{5}}{2}\]et \[z+\frac{1}{z} = \frac{-1-\sqrt{5}}{2}\]ce qui fait en multipliant par \(z\) de chaque côté\[z^{2} +1 = \left(\frac{-1+\sqrt{5}}{2}\right)z\] et \[z^{2}+1=\left(\frac{-1-\sqrt{5}}{2}\right)z\]puis en regroupant les termes du même côté \[z^{2}+\left(\frac{1-\sqrt{5}}{2}\right)z + 1 = 0\]et \[z^{2}+\left(\frac{1+\sqrt{5}}{2}\right)z + 1 = 0\]Deux autres équations quadratiques ! En utilisant la formule quadratique, on trouve que les solutions de la première sont \[z = \left(\frac{1}{2(1)}\right)\left(\frac{-1+\sqrt{5}}{2}\pm\sqrt{\left(\frac{1-\sqrt{5}}{2}\right)^{2}-4(1)(1)}\right)\]ou en simplifiant un peu \[z = \frac{-1+\sqrt{5}}{4}\pm\sqrt{\frac{-5-\sqrt{5}}{8}}\]Or comme \[-5-\sqrt{5}<0\]on obtient \[z = \frac{-1+\sqrt{5}}{4}\pm\left(\sqrt{\frac{5+\sqrt{5}}{8}}\right)i\]

De la même manière, on trouve les solutions de la deuxième équation \[z = \left(\frac{1}{2(1)}\right)\left(\frac{-1-\sqrt{5}}{2}\pm\sqrt{\left(\frac{1+\sqrt{5}}{2}\right)^{2}-4(1)(1)}\right)\]ou en simplifiant un peu \[z = \frac{-1-\sqrt{5}}{4}\pm\sqrt{\frac{-5+\sqrt{5}}{8}}\]Et comme encore une fois \[-5+\sqrt{5}<0\]on obtient \[z = \frac{-1-\sqrt{5}}{4}\pm\left(\sqrt{\frac{5-\sqrt{5}}{8}}\right)i\]

Avec le premier couple de solutions, \[z = \frac{-1+\sqrt{5}}{4}\pm\left(\sqrt{\frac{5+\sqrt{5}}{8}}\right)i\]on remarque que \[\frac{-1+\sqrt{5}}{4}>0\]et \[\pm\sqrt{\frac{5+\sqrt{5}}{8}} \; \mathrel{\substack{>\\<}} \; 0\]et donc on déduit que \begin{align*}\cos\left(\frac{2\pi}{5}\right) &= \frac{-1+\sqrt{5}}{4} \\ \\ \sin\left(\frac{2\pi}{5}\right) &= \sqrt{\frac{5+\sqrt{5}}{8}}\end{align*}et \begin{align*}\cos\left(\frac{8\pi}{5}\right) &= \frac{-1+\sqrt{5}}{4} \\ \\ \sin\left(\frac{8\pi}{5}\right)&=-\sqrt{\frac{5+\sqrt{5}}{8}}\end{align*}Avec le deuxième couple de solutions, \[z = \frac{-1-\sqrt{5}}{4}\pm\left(\sqrt{\frac{5-\sqrt{5}}{8}}\right)i\]cette fois-ci on constate que \[\frac{-1-\sqrt{5}}{4}<0\]et que \[\pm\sqrt{\frac{5-\sqrt{5}}{8}}\; \mathrel{\substack{>\\<}} \; 0\]et cela nous permet d’obtenir \begin{align*}\cos\left(\frac{4\pi}{5}\right)&=\frac{-1-\sqrt{5}}{4} \\ \\ \sin\left(\frac{4\pi}{5}\right)&=\sqrt{\frac{5-\sqrt{5}}{8}}\end{align*}et \begin{align*}\cos\left(\frac{6\pi}{5}\right)&=\frac{-1-\sqrt{5}}{4} \\ \\ \sin\left(\frac{6\pi}{5}\right)&=-\sqrt{\frac{5-\sqrt{5}}{8}}\end{align*}On aurait pu avoir recours aux formules pour les angles doubles en utilisant au départ les valeurs du sinus et du cosinus de π/5 mais cette avenue ne nous aurait pas donner le loisir de résoudre une équation quartique dans \(\mathbb{C}\) !

Référence : R. Courant, H. Robbins et I. Stewart (1996), What is mathematics ?

Voici une courte anecdote de Lord Kelvin, professeur.

Once when lecturing he used the word “mathematician,” and then interrupting himself asked his class: “Do you know what a mathematician is?” Stepping to the blackboard he wrote upon it :

Then, putting his finger on what he had written, he turned to his class and said: “A mathematician is one to whom that is as obvious as that twice two makes four is to you. Liouville was a mathematician.” Then he resumed his lecture.

S. P. Thompson, The Life of William Thomson, Baron Kelvin of Largs, p. 1139