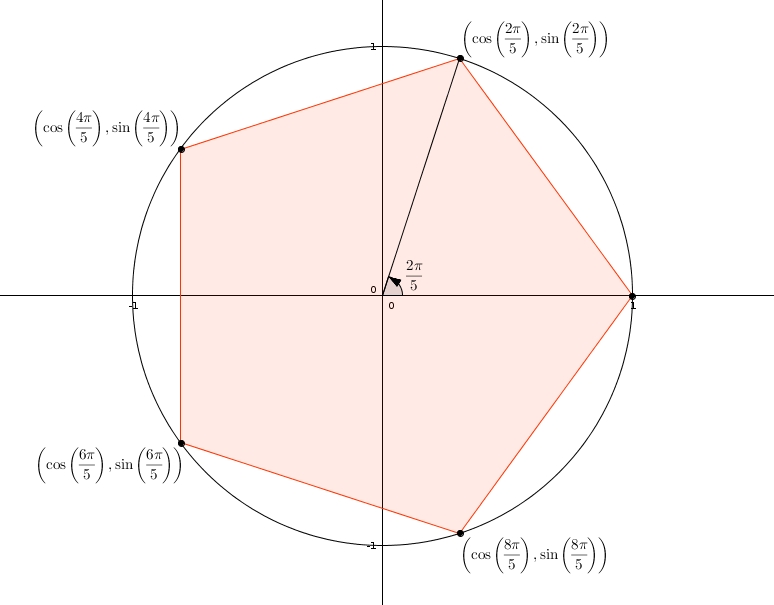
On cherche les valeurs du sinus et du cosinus pour les angles suivants : \(\frac{2\pi}{5}\), \(\frac{4\pi}{5}\), \(\frac{6\pi}{5}\) et \(\frac{8\pi}{5}\).
Dans le cercle trigonométrique, ces points correspondent aux sommets d’un pentagone régulier inscrit. Dans le plan complexe, les sommets de ce pentagone inscrit dans le cercle d’équation \[z\bar{z} = 1\]correspondent aux solutions de l’équation \[z^{5}-1=0\]c’est-à-dire aux racines cinquièmes de l’unité. L’une de ces racines est évidemment \(1\). En effectuant la longue division par \(z-1\), on peut vérifier que \[(z-1)(z^{4}+z^{3}+z^{2}+z+1)=0\]ou, si \(z \neq 1\), \[z^{4} + z^{3}+z^{2}+z+1=0\]Il faut donc résoudre cette équation quartique. Mince affaire ! Heureusement, on peut ici appliquer un petit truc. Si \(z \neq 0\), on divise par \(z^{2}\) \[z^{2}+z^{1}+1+\frac{1}{z^{1}}+ \frac{1}{z^{2}}=0\]et on réarrange les termes \[z^{2}+\frac{1}{z^{2}}+z+\frac{1}{z}+1=0\]En remarquant que \[\left(z + \frac{1}{z}\right)^{2}= z^{2}+\frac{1}{z^{2}}+2\]l’équation précédente devient \begin{align*} z^{2}+\frac{1}{z^{2}}+z+\frac{1}{z}+1&=0 \\ \\ z^{2}+\frac{1}{z^{2}}+2 + z + \frac{1}{z}+1-2 &=0 \\ \\ \left(z + \frac{1}{z}\right)^{2} + \left(z + \frac{1}{z}\right)-1 &=0\end{align*}une équation du deuxième degré en \(\left(z + \frac{1}{z}\right)\) ! En utilisant la formule quadratique, on trouve que les solutions sont\[z + \frac{1}{z} = \frac{-1+\sqrt{5}}{2}\]et \[z+\frac{1}{z} = \frac{-1-\sqrt{5}}{2}\]ce qui fait en multipliant par \(z\) de chaque côté\[z^{2} +1 = \left(\frac{-1+\sqrt{5}}{2}\right)z\] et \[z^{2}+1=\left(\frac{-1-\sqrt{5}}{2}\right)z\]puis en regroupant les termes du même côté \[z^{2}+\left(\frac{1-\sqrt{5}}{2}\right)z + 1 = 0\]et \[z^{2}+\left(\frac{1+\sqrt{5}}{2}\right)z + 1 = 0\]Deux autres équations quadratiques ! En utilisant la formule quadratique, on trouve que les solutions de la première sont \[z = \left(\frac{1}{2(1)}\right)\left(\frac{-1+\sqrt{5}}{2}\pm\sqrt{\left(\frac{1-\sqrt{5}}{2}\right)^{2}-4(1)(1)}\right)\]ou en simplifiant un peu \[z = \frac{-1+\sqrt{5}}{4}\pm\sqrt{\frac{-5-\sqrt{5}}{8}}\]Or comme \[-5-\sqrt{5}<0\]on obtient \[z = \frac{-1+\sqrt{5}}{4}\pm\left(\sqrt{\frac{5+\sqrt{5}}{8}}\right)i\]
De la même manière, on trouve les solutions de la deuxième équation \[z = \left(\frac{1}{2(1)}\right)\left(\frac{-1-\sqrt{5}}{2}\pm\sqrt{\left(\frac{1+\sqrt{5}}{2}\right)^{2}-4(1)(1)}\right)\]ou en simplifiant un peu \[z = \frac{-1-\sqrt{5}}{4}\pm\sqrt{\frac{-5+\sqrt{5}}{8}}\]Et comme encore une fois \[-5+\sqrt{5}<0\]on obtient \[z = \frac{-1-\sqrt{5}}{4}\pm\left(\sqrt{\frac{5-\sqrt{5}}{8}}\right)i\]
Avec le premier couple de solutions, \[z = \frac{-1+\sqrt{5}}{4}\pm\left(\sqrt{\frac{5+\sqrt{5}}{8}}\right)i\]on remarque que \[\frac{-1+\sqrt{5}}{4}>0\]et \[\pm\sqrt{\frac{5+\sqrt{5}}{8}} \; \mathrel{\substack{>\\<}} \; 0\]et donc on déduit que \begin{align*}\cos\left(\frac{2\pi}{5}\right) &= \frac{-1+\sqrt{5}}{4} \\ \\ \sin\left(\frac{2\pi}{5}\right) &= \sqrt{\frac{5+\sqrt{5}}{8}}\end{align*}et \begin{align*}\cos\left(\frac{8\pi}{5}\right) &= \frac{-1+\sqrt{5}}{4} \\ \\ \sin\left(\frac{8\pi}{5}\right)&=-\sqrt{\frac{5+\sqrt{5}}{8}}\end{align*}Avec le deuxième couple de solutions, \[z = \frac{-1-\sqrt{5}}{4}\pm\left(\sqrt{\frac{5-\sqrt{5}}{8}}\right)i\]cette fois-ci on constate que \[\frac{-1-\sqrt{5}}{4}<0\]et que \[\pm\sqrt{\frac{5-\sqrt{5}}{8}}\; \mathrel{\substack{>\\<}} \; 0\]et cela nous permet d’obtenir \begin{align*}\cos\left(\frac{4\pi}{5}\right)&=\frac{-1-\sqrt{5}}{4} \\ \\ \sin\left(\frac{4\pi}{5}\right)&=\sqrt{\frac{5-\sqrt{5}}{8}}\end{align*}et \begin{align*}\cos\left(\frac{6\pi}{5}\right)&=\frac{-1-\sqrt{5}}{4} \\ \\ \sin\left(\frac{6\pi}{5}\right)&=-\sqrt{\frac{5-\sqrt{5}}{8}}\end{align*}On aurait pu avoir recours aux formules pour les angles doubles en utilisant au départ les valeurs du sinus et du cosinus de π/5 mais cette avenue ne nous aurait pas donner le loisir de résoudre une équation quartique dans \(\mathbb{C}\) !
Référence : R. Courant, H. Robbins et I. Stewart (1996), What is mathematics ?