On connait beaucoup de choses sur les médianes, les hauteurs, les médiatrices ou les bissectrices d’un triangle. Le théorème de Stewart concerne les segments internes du triangles joignant un sommet à son côté opposé d’une manière quelconque . Considérons le triangle suivant :
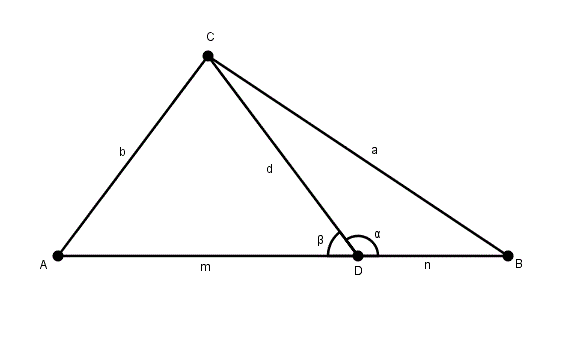
Remarquons que\[\alpha + \beta = 180^{\circ}\]et donc que \[\cos(\alpha) = -\cos(\beta) \qquad (1)\]Avec la loi des cosinus, dans le triangle \(ADC\), on trouve\[b^2 = m^2 + d^2 \ – \ 2md \cdot \cos(\beta)\]En isolant le cosinus, on obtient\[\cos(\beta) = \frac{-b^2 + m^2 + d^2}{2md}\]Avec la loi des cosinus, mais cette fois-ci dans le triangle \(CDB\), on obtient\[a^2 = n^2 + d^2 \ – \ 2nd\cdot \cos(\alpha)\]En isolant le cosinus, on obtient\[\cos(\alpha) = \frac{-a^2 + n^2 + d^2}{2nd}\]Ce qui implique en vertu de \((1)\) que\[-\cos(\beta) = \frac{-a^2 + n^2 + d^2}{2nd}\]Et donc que\[\cos(\beta) = \frac{a^2 \ – \ n^2\ – \ d^2}{2nd}\]En égalant les deux expressions, on obtient\[\frac{-b^2 + m^2 + d^2}{2md} = \frac{a^2 \ – \ n^2 \ – \ d^2}{2nd}\]Puis en mettant sur dénominateur commun\[\frac{-b^2n + m^2n + d^2n}{2mnd} = \frac{a^2m \ – \ n^2m \ – \ d^2m}{2mnd}\]ce qui fait\[-b^2n + m^2n + d^2n = a^2m \ – \ n^2m \ – \ d^2m\]ou de manière équivalente\[d^2n + d^2m + m^2n + n^2m = a^2m + b^2n\]En effectuant une mise en évidence double, on obtient\[d^2(n + m) + nm(m + n) = a^2m + b^2n\]puis\[(d^2 + nm)(m+n) = a^2m + b^2n\]Et comme\[c = m + n\]on obtient finalement\[c(d^2 + nm) = a^2m + b^2n\]Voilà ! Le théorème de Stewart.
Référence : Alfred S. Posamentier et Salkind, Charles T., Challenging Problems In Geometry (1996)
One thought on “Le théorème de Stewart”