Category: Mathématiques

La forme canonique de la fonction exponentielle est \[g(x) = a\cdot c^{b(x-h)}+k\]où \(c\) est la base de la fonction de la fonction exponentielle (strictement positive et différente de \(1\)).  On utilise les lettres usuelles \(a\), \(b\), \(h\), \(k\) pour désigner les paramètres multiplicatifs et additifs des variables dépendantes et indépendantes.  Comme avec bien d’autres fonctions, il s’avère que certains paramètres sont superflus.  En transformant le produit à l’exposant en exponentiation, on obtient \[g(x) = a\cdot \left(c^{b}\right)^{(x-h)}+k\]Il nous est donc possible de choisir une nouvelle base, \(c_{1}\), telle que \[c_{1} = c^{b}\]Notre fonction initiale devient alors \[g(x) = a\cdot \left(c_{1}\right)^{(x-h)}+k\]En transformant la somme à l’exposant en produit de deux puissances de même base on obtient \[g(x) = a\cdot \left(c_{1}\right)^{x}\cdot \left(c_{1}\right)^{-h}+k\]que je réécris comme \[g(x) = a\cdot \left(c_{1}\right)^{-h}\cdot \left(c_{1}\right)^{x}+k\]Il nous est maintenant possible de choisir un nouveau paramètre \(a\), appelons-le \(a_{1}\), tel que \[a_{1}=a\cdot\left(c_{1}\right)^{-h}\]Notre fonction devient alors \[g(x)=a_{1}\cdot\left(c_{1}\right)^{x}+k\]que j’appellerai la forme canonique réduite de la fonction exponentielle.  Il est donc toujours possible de poser \(b=1\) et \(h=0\) dans le cas d’une fonction exponentielle en jouant avec le paramètre \(a\) et la base \(c\).

Qu’en est-il de la fonction logarithmique, la réciproque de la fonction exponentielle ?  La forme canonique de la fonction logarithmique est \[f(x) = a\log_{c}\left(b(x-h)\right)+k\]où, encore une fois, \(c\) est la base de la fonction logarithmique (strictement positive et différente de \(1\)).

Cette fonction possèdent-elles des paramètres superflus ?  Avec l’exponentielle, nous avions d’abord effectué un changement de base.  Est-il possible d’emprunter une démarche semblable ? On change la base de la fonction logarithmique pour la nouvelle base \(c_{1}\).  La loi du changement de base avec les logarithmes nous donne \[f(x) = a\left(\frac{\log_{c_{1}}\left(b(x-h)\right)}{\log_{c_{1}}(c)}\right) + k\]que je réécris comme \[f(x) = \frac{a}{\log_{c_{1}}(c)} \cdot \log_{c_{1}}\left(b(x-h)\right) + k\]En posant le coefficient égal à \(1\), \[\frac{a}{\log_{c_{1}}(c)}=1\]et en isolant le logarithme, on obtient \[a = \log_{c_{1}}(c)\]En transformant sous la forme exponentielle on obtient \[\left(c_{1}\right)^{a} =c\]Et en isolant \(c_{1}\) on obtient \[c_{1} = c^{\frac{1}{a}}\]c’est-à-dire \[c_{1} = \sqrt[a]{c}\]si \(a\) est positif et \[c_{1} = \sqrt[-a]{\frac{1}{c}}\]si \(a\) est négatif.

En choisissant la bonne base, il est donc toujours possible de rendre le paramètre \(a=1\). En effet, en choisissant \(c_{1}\) de telle manière, notre fonction initiale devient \[f(x) = \log_{c_{1}}\left(b(x-h)\right)+k\]Notons ensuite que par définition de logarithme, on a \[k = \log_{c_{1}}\left(\left(c_{1}\right)^{k}\right)\](et, au passage, pas de problème si \(k\) est négatif).

En remplaçant dans \[f(x) = \log_{c_{1}}\left(b(x-h)\right)+k\]on obtient \[f(x) = \log_{c_{1}}\left(b(x-h)\right) + \log_{c_{1}}\left(\left(c_{1}\right)^{k}\right)\]En exprimant la somme des deux logarithmes avec le logarithme du produit on obtient \[f(x) = \log_{c_{1}}\left(b\cdot \left(c_{1}\right)^{k}\cdot (x-h)\right)\]En choisissant un nouveau paramètre \(b\), appelons-le \(b_{1}\), tel que \[b_{1}= b\cdot \left(c_{1}\right)^{k}\]notre fonction initiale devient \[f(x) = \log_{c_{1}}\left(b_{1}(x-h)\right)\]que j’appelle la forme canonique réduite de la fonction logarithmique.

Si on place un capital initial \(C_{0}\) à un taux d’intérêt annuel \(i\) composé \(n\) fois par année, alors après avoir composé \(t\) fois l’intérêt, on aura accumulé un (fameux) montant \(C(t)\) de \[C(t) = C_{0}\left(1+\frac{i}{n}\right)^{t}\]C’est la formule bien connue de l’intérêt composé.  Par exemple, si on place \(5\, 000\) dollars pendant \(10\) ans à un taux d’intérêt annuel de \(2\%\) (donc \(i = 0,\!02\)) composé chaque mois (donc \(n=12\)), on obtient au bout des \(10\) ans (c’est-à-dire après avoir composé les intérêts \(12 \times 10 = 120\) fois) \[C(120) =5000 \left(1+\frac{0,\!02}{12}\right)^{12\cdot 10} \approx 6\,106,\!00\]C’est environ \(1\,106\) dollars de plus, une augmentation de près de \(22\%\) par rapport au capital initialement investi !  Pas mal !  C’est aussi \(106\) dollars de plus que si on avait placé cet argent à intérêt simple. Vous me direz : « Placer 5000$ en 2010 pendant 10 ans à ton âge, c’est de la science-fiction ! »

En effet, la (ma ?) tendance actuelle est plutôt à l’emprunt de capital !  Et lorsqu’on emprunte, on doit éventuellement rembourser.  Supposons que l’on rembourse, à chaque fois que l’on compose les intérêts (chaque trimestre ? mois ? semaine ?), un certain montant \(P\).  Et considérons une fonction \(f\) qui exprime notre capital dû.

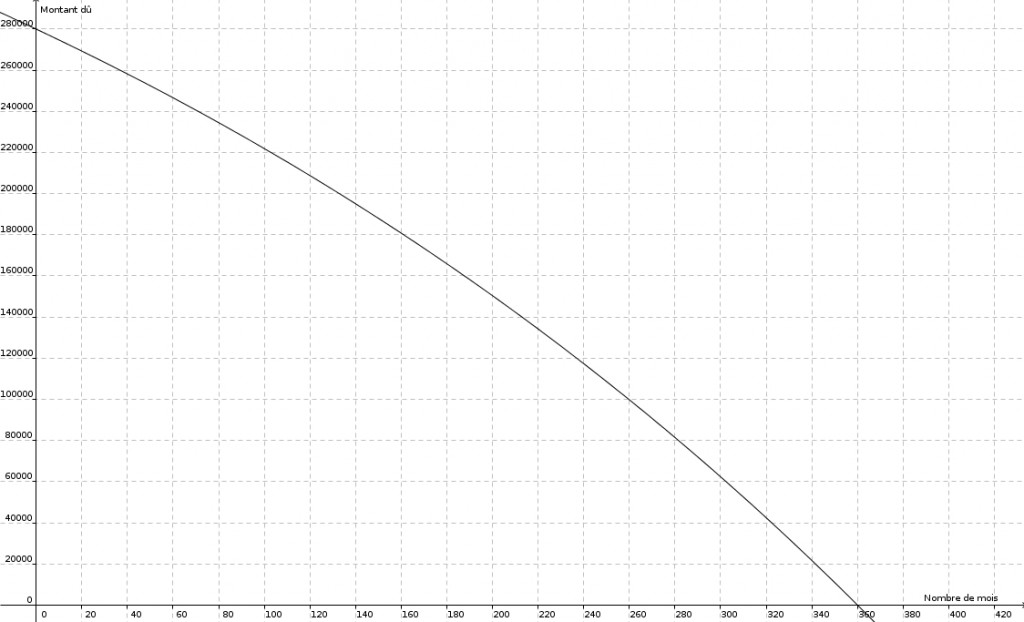
Au départ on a tout simplement \[f(0) = C_{0}\]Après un premier calcul des intérêts, \(\left(1 +\frac{i}{n}\right)\), on rembourse un montant \(P\). \[f(1) = C_{0}\left(1 + \frac{i}{n}\right)-P\]Au deuxième versement, c’est \[f(2) = \left(C_{0}\left(1 + \frac{i}{n}\right)-P\right)\left(1 + \frac{i}{n}\right)-P\]En distribuant le facteur \(\left(1+\frac{i}{n}\right)\) on obtient \[f(2) = C_{0}\left(1+\frac{i}{n}\right)^{2}-P\left(1 + \frac{i}{n}\right)-P\]Au troisième,\[f(3) = \left(C_{0}\left(1 + \frac{i}{n}\right)^{2}-P\left(1+\frac{i}{n}\right)-P\right)\left(1 + \frac{i}{n}\right)-P\]et encore une fois en distribuant, \[f(3) = C_{0}\left(1+\frac{i}{n}\right)^{3}-P\left(1+\frac{i}{n}\right)^{2}-P\left(1+\frac{i}{n}\right)-P\]Au quatrième calcul des intérêts, \[f(4)=\left(C_{0}\left(1+\frac{i}{n}\right)^{3}-P\left(1+\frac{i}{n}\right)^{2}-P\left(1+\frac{i}{n}\right)-P\right)\left(1+\frac{i}{n}\right)-P\]et en distribuant, \[f(4) = C_{0}\left(1+\frac{i}{n}\right)^{4}-P\left(1+\frac{i}{n}\right)^{3}-P\left(1+\frac{i}{n}\right)^{2}-P\left(1+\frac{i}{n}\right)-P\]Une tendance se dégage.  Il apparait de plus en plus clair qu’au \(t\)^e calcul des intérêts, on aura \[f(t) = C_{0}\left(1+\frac{i}{n}\right)^{t}-P\left(1+\frac{i}{n}\right)^{t-1}\ – \ \dots \ – \ P\left(1+\frac{i}{n}\right)^{2}-P\left(1+\frac{i}{n}\right)-P\]Une mise en évidence simple de \(-P\) nous donne \[f(t) = C_{0}\left(1+\frac{i}{n}\right)^{t}-P\left(\left(1+\frac{i}{n}\right)^{t-1} \ + \ \dots \ + \ \left(1 + \frac{i}{n}\right)^{2}+\left(1+\frac{i}{n}\right) + 1\right)\]L’expression dans la grande parenthèse est une série géométrique finie de premier terme 1 et de raison (1 + i/n).  Nous pouvons exprimer sa somme de façon plus concise.  On obtient \[f(t) = C_{0}\left(1+\frac{i}{n}\right)^{t}-P\left(\frac{1-\left(1+\frac{i}{n}\right)^{t}}{1-\left(1+\frac{i}{n}\right)}\right)\]Enfin, une petite simplification nous donne \[f(t)=C_{0}\left(1+\frac{i}{n}\right)^{t}-P\left(\frac{1-\left(1+\frac{i}{n}\right)^{t}}{1-1-\frac{i}{n}}\right)\]puis \[f(t) = C_{0}\left(1+\frac{i}{n}\right)^{t}+P\left(\frac{n}{i}\right)\left(1-\left(1+\frac{i}{n}\right)^{t}\right)\]Voilà donc l’expression recherchée.  Maintenant, comment calculer la valeur de \(P\) afin qu’à terme, on ait remboursé la totalité de notre emprunt ?  Posons \[f(t) = 0\]On a alors \[C_{0}\left(1+\frac{1}{n}\right)^{t}+P\left(\frac{n}{i}\right)\left(1-\left(1+\frac{i}{n}\right)^{t}\right) = 0\]On soustrait \(C_{0}\left(1+\frac{i}{n}\right)^{t}\)de chaque côté de l’égalité \[P\left(\frac{n}{i}\right)\left(1-\left(1+\frac{i}{n}\right)^{t}\right)=-C_{0}\left(1+\frac{i}{n}\right)^{t}\]puis on divise \[P=\frac{-C_{0}\left(\frac{i}{n}\right)\left(1+\frac{i}{n}\right)^{t}}{1-\left(1+\frac{i}{n}\right)^{t}}\]En multipliant par \(-1\) en haut et en bas, on obtient l’expression légèrement plus élégante suivante \[P= \frac{C_{0}\left(\frac{i}{n}\right)\left(1+\frac{i}{n}\right)^{t}}{\left(1+\frac{i}{n}\right)^{t}-1}\]Cette dernière formule nous donne la valeur de \(P\) en fonction de \(C_{0}\), \(i\), \(n\) et \(t\).  Supposons que l’on emprunte \(280\, 000\) dollars sur une période de \(30\) ans à un taux annuel de \(2,\!5\%\), composé chaque mois, le remboursement mensuel s’élèvera à \[P = \frac{280\,000\left(\frac{0,025}{12}\right)\left(1+\frac{0,025}{12}\right)^{(12\cdot 30)}}{\left(1+\frac{0,025}{12}\right)^{(12\cdot 30)}-1} \approx 1\,106,\!34\]Et l’expression \[f(t) = C_{0}\left(1+\frac{i}{n}\right)^{t}+P\left(\frac{n}{i}\right)\left(1-\left(1+\frac{i}{n}\right)^{t}\right)\]ou, de manière équivalente, \[f(t) = \left(C_{0}-P\cdot \left(\frac{n}{i}\right)\right)\cdot\left(1+\frac{i}{n}\right)^{t}+P\cdot\left(\frac{n}{i}\right)\]nous permet alors de représenter graphiquement la situation (le montant dû en fonction du temps)

La formule de l’intérêt composé est aussi une occasion de découvrir une constante mathématique bien connue.

On décide de placer notre capital pour une durée de \(s\) année.  Au bout de ces \(s\) années, avec des intérêts composés \(n\) fois par année, on aura effectué \(n\cdot s\) calculs d’intérêt (\(t = ns\)).  Supposons que l’on place \(5\,000\)$ pendant \(10\) ans à un taux d’intérêt annuel de \(2\%\), composé une seule fois par année.  Après \(10\) ans on obtient \[5\,000\left(1+\frac{0,\!02}{1}\right)^{1\cdot 10} \approx 6\,094,\!97\]Si les intérêts sont calculés chaque trimestre (\(n=4\)), on obtient \[5\,000\left(1+\frac{0,\!02}{4}\right)^{4\cdot 10} \approx 6\,103,\!97\]c’est-à-dire environ \(9\) dollars de plus (par rapport à \(n=1\)).  En calculant les intérêts chaque mois, on obtient \[5\,000\left(1+\frac{0,\!02}{12}\right)^{12\cdot 10} \approx 6\,106,\!00\]résultat déjà calculé ci-haut.  C’est un peu plus de \(2\) dollars de plus que pour des intérêts calculés chaque trimestre.  On peut conjecturer que plus l’intérêt est calculé un grand nombre de fois par année, plus le montant accumulé sera grand sur cette période.  Cependant, l’impact  semble devenir de plus en plus minime.  Si les intérêts sont calculés chaque jour, on obtient \[5\,000 \left(1+\frac{0,\!02}{365}\right)^{365\cdot 10} \approx 6\,106,\!98\]c’est-à-dire une augmentation de seulement \(98\) cents sur une période de \(10\) ans (par rapport à des intérêts composés chaque mois).  Des intérêts composés chaque seconde ?  Pourquoi pas !\[5\,000 \left(1+ \frac{0,\!02}{31\,536\,000}\right)^{31\,536\,000 \cdot 10} \approx 6\,107,\!02\]Avec les montants en jeu, on gagne… \(4\) cents !  Sur \(10\) ans !  Dix ans pendant lesquels chaque année on calcule les intérêts plus de \(31\) millions de fois.  Le phénomène semble se rapprocher d’une limite.  Qu’arrive-t-il alors à cette expression \[f(s) = C_{0}\left(1+\frac{i}{n}\right)^{ns}\]lorsqu’on fait tendre \(n\) à l’infini ?  En faisant tendre \(n\) à l’infini, on considère des intérêts composés de façon continue.  Afin de rendre les choses claires et élégantes, on introduit une nouvelle variable \(u\) telle que \[u =\frac{n}{i}\]Si \[n\to \infty\]alors il est clair que \[u \to \infty\]lui aussi.  Cela implique également que \[n = ui\]et \[\frac{i}{n} = \frac{1}{u}\]On peut donc réécrire \[f(s) = C_{0}\left(1 + \frac{i}{n}\right)^{ns}\]lorsque \[n\to \infty\]comme \[f(s) = C_{0}\left(1+\frac{1}{u}\right)^{uis}\]lorsque \[n\to \infty\]En transformant le produit à l’exposant en exponentiation on obtient \[f(s) = C_{0}\left(\left(1+\frac{1}{u}\right)^{u}\right)^{is}\]Et comme \[u\to \infty\]on a \[\left(1+\frac{1}{u}\right)^{u} \to e\]La base naturelle \(e\) fait son apparition !  On obtient donc plus simplement \[f(s) = C_{0}\, e^{is}\]pour calculer les intérêts composés de façon continue.

On considère la série géométrique (finie) suivante, de premier terme \(a\) et de raison \(r\), dont la somme (c’est une série finie) est\[S = \sum_{k=0}^{n} ar^{k} = a + ar + ar^2\ + \ \dots \ + \ ar^{n-1} + ar^n\]Le truc bien connu pour exprimer \(S\) de façon plus concise est le suivant.  On multiplie d’abord chaque côté de l’équation par \(r\) \[rS = ar + ar^2 + ar^3 \ + \ \dots \ + ar^n + ar^{n+1}\] On soustrait la deuxième équation de la première.  Tous les termes s’annulent sauf deux.\[S-rS = a-ar^{n+1}\] Une mise en évidence de \(S\) à gauche et de \(a\) à droite nous donne\[S(1-r) = a\left(1-r^{n+1}\right)\]En divisant par \((1-r)\) de chaque côté on obtient l’expression de la somme recherchée\[S = \sum_{k=0}^{n}ar^k = a\frac{1-r^{n+1}}{1-r}\]

Qu’en est-il d’une série géométrique infinie ?  La série converge vers une valeur \(S\) si et seulement si la valeur absolue de la raison est strictement inférieure à \(1\).\[\left|r\right|<1\]

On peut obtenir cette valeur en faisant tendre \(n\) vers l’infini\[S = \lim_{n \to \infty}\sum_{k=0}^{n}ar^k = \lim_{n \to \infty}a\frac{1-r^{n+1}}{1-r}\]Or, comme\[\left|r\right|<1\]on a\[r^{n+1}\to 0\]lorsque\[n\to \infty\]ce qui fait\[S = \lim_{n\to \infty} \sum_{k = 0}^{n}ar^k = \lim_{n\to \infty} a\frac{1-r^{n+1}}{1-r} = a\frac{1}{1-r}\]Cette dernière expression nous permet de trouver les sommes de séries géométriques infinies telles que\[\lim_{n\to \infty}\sum_{k=0}^{n}\left(\frac{1}{2}\right)^k = 1 + \frac{1}{2}+\frac{1}{4} + \frac{1}{8}+ \frac{1}{16}+\dots=1\cdot \frac{1}{1-\frac{1}{2}} = 2\]ou\[\lim_{n\to \infty}\sum_{k=0}^{n}\left(-\frac{1}{3}\right)^k = 1-\frac{1}{3}+\frac{1}{9}-\frac{1}{27}+\dots=1\cdot\frac{1}{1-\left(-\frac{1}{3}\right)} = \frac{3}{4}\]cette dernière étant une série géométrique infinie alternée.

Voici comment Jakob Bernoulli, dans son Tractatus de seriebus infinitis earumque summa finita, écrit en 1689, somme les séries géométriques.  Il définit d’abord une série géométrique comme une somme de termes positifs\[S = A + B + C+\dots+D+E\]dans laquelle\[\frac{A}{B}=\frac{B}{C}=\dots=\frac{D}{E}\]Il énonce ensuite ceci : “Dans une progression géométrique A, B, C, … , D, E, le premier terme est au deuxième ce que la somme de tous les termes sauf le dernier est à la somme de tous les termes sauf le premier.”

Afin de bien comprendre cet énoncé, posons (conformément à notre notation habituelle)\[\frac{A}{B} = \frac{1}{r}\]ce qui implique que\[Ar = B, \ Br = C, \ \dots \ , \ Dr = E\]ou\[Ar = B, \ Ar^2 = C, \ \dots \ , Ar^n = E\]L’énoncé peut maintenant être vérifié facilement puisque

On multiplie ensuite le numérateur et le dénominateur\[\frac{A}{B} = \frac{A}{Ar} = \frac{A\left(1 + r + r^2+\dots+r^{n-1}\right)}{Ar\left(1+r+r^2+\dots+r^{n-1}\right)}\]En distribuant dans les parenthèses on obtient\[\frac{A}{B} = \frac{A + Ar + Ar^2+\dots+Ar^{n-1}}{Ar + r^2 + r^3+\dots+Ar^n}\]ce qui fait\[\frac{A}{B} = \frac{A+B+C+\dots+D}{B+C+\dots+E}\]c’est-à-dire que “dans une progression géométrique A, B, C, … , D, E, le premier terme est au deuxième ce que la somme de tous les termes sauf le dernier est à la somme de tous les termes sauf le premier.”

En considérant la somme \(S\) de la série géométrique, Jakob remarque que\[A+B+C+\dots+D = S-E\]et\[B+C+\dots+E = S-A\]Il remplace donc dans l’expression précédente et obtient\[\frac{A}{B} = \frac{S-E}{S-A}\]qu’il s’applique ensuite à résoudre pour \(S\) \[A(S-A)=B(S-E)\]Puis en distribuant de chaque côté\[AS-A^2 = BS-BE\]Regroupant ensuite les termes en \(S\) à gauche\[AS-BS =A^2-BE\]et après la mise en évidence\[S(A-B) = A^2-BE\]il obtient le résultat recherché\[S=\frac{A^2-BE}{A-B}\]Cette expression concise de la somme de la série géométrique utilise la premier terme \(A\) , le deuxième terme \(B\) et le dernier terme \(E\), contrairement à la forme moderne qui utilise le premier terme \(a\), le nombre de terme \(n\) et la raison \(r\).  Jakob observe par la suite que si le rapport des termes successifs est plus petit que \(1\), le dernier terme doit s’approcher de \(0\).  Pour une série géométrique infinie, il pose donc son “dernier” terme, \(E\), égal à \(0\).\[E = 0\]et il obtient comme somme d’une série géométrique infinie de premier terme \(A\) et de deuxième terme \(B\)\[S = \frac{A^2}{A-B}\]