Category: Mathématiques

Embrace your inner geekiness

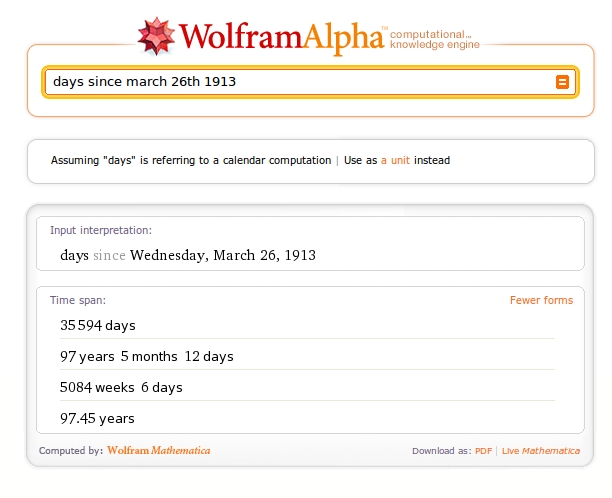
C’est mon ami Monsieur C. qui m’a fait découvrir Wolfram | Alpha au moment de son lancement. Il l’utilisait entre autres pour calculer ses anniversaires de jours (incidemment, je viens tout juste de fêter mon 10000^ième anniversaire). J’ai découvert depuis qu’on pouvait faire pas mal plus “geek”. On peut célébrer nos anniversaires “premiers”.

Sur Wolfram | Alpha, entrez “days since [votre date de naissance]”. Pál Erdős, s’il était encore vivant, pourrait entrer :

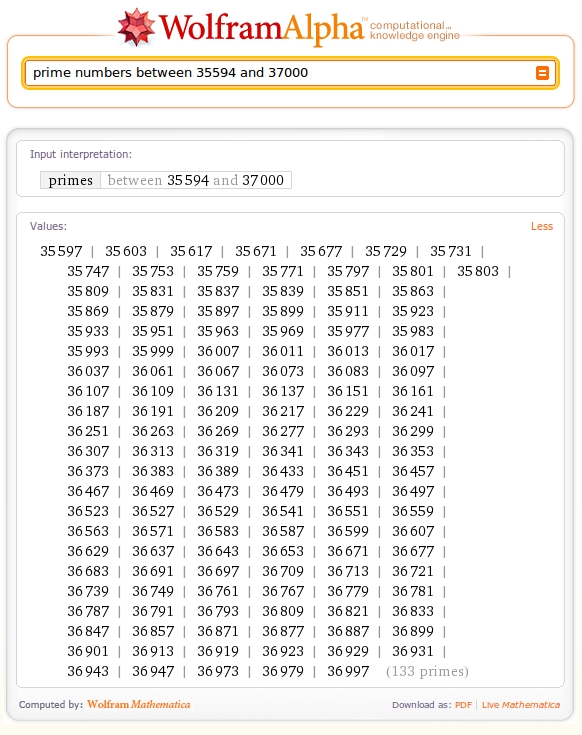
On demande ensuite à Wolfram | Alpha la liste des nombres premiers aux alentours de 35594. On entre “prime numbers between […] and […]”.

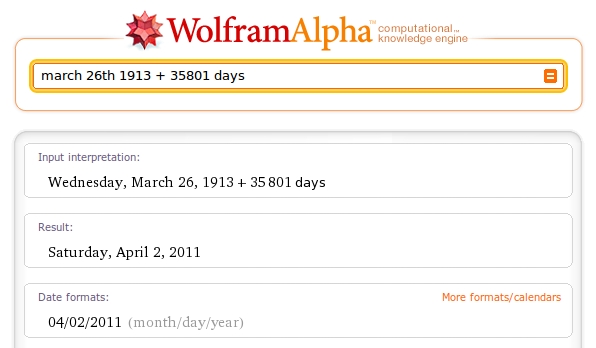
M. Erdős célèbrerait donc plusieurs anniversaires « premiers» dans les prochains jours (mais n’aurait probablement pas besoin d’un outil comme Wolfram | Alpha pour les calculer). Si vous trouvez que les anniversaires « premiers » sont trop nombreux, vous pouvez ne célébrer que les anniversaires « premiers jumeaux ». M. Erdős célèbrerait ses prochains anniversaires « premiers jumeaux » à ses 35801^ième et 35803^ième jours de naissance soit…

les samedi 2 avril 2011 et lundi 4 avril 2011.  La conjecture des nombres premiers jumeaux affirme qu’il existe une infinité de ces nombres premiers \(p\) tels que \(p+2\) est aussi premier.  Erdős s’est intéressé à cette conjecture mais elle reste toujours à démontrer.  Si les nombres premiers jumeaux sont encore trop nombreux à votre goût, vous pouvez ne vous intéresser qu’aux nombres premiers qui sont aussi des palindromes.  On ne sait pas encore aujourd’hui s’il existe une infinité de ces nombres mais en voici quelques uns…

2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, 10301, 10501, 10601, 11311, 11411, 12421, 12721, 12821, 13331, 13831, 13931, 14341, 14741, 15451, 15551, 16061, 16361, 16561, 16661, 17471, 17971, 18181, 18481, 19391, 19891, 19991, 30103, 30203, 30403, 30703, 30803, 31013, 31513, 32323, 32423, 33533, 34543, 34843, 35053, 35153, 35353, 35753, 36263, 36563, 37273, 37573, 38083, 38183, 38783, 39293, 70207, 70507, 70607, 71317, 71917, 72227, 72727, 73037, 73237, 73637, 74047, 74747, 75557, 76367, 76667, 77377, 77477, 77977, 78487, 78787, 78887, 79397, 79697, 79997, 90709, 91019, 93139, 93239, 93739, 94049, 94349, 94649, 94849, 94949, 95959, 96269, 96469, 96769, 97379, 97579, 97879, 98389, 98689 …

 

Référence :http://travelsinamathematicalworld.blogspot.com/2010/08/prime-birthdays-via-wolframalpha.html via http://jd2718.wordpress.com/2010/09/03/carnival-of-mathematics-69/

On considère la fraction continue simple la plus (c’est bien le cas de le dire) simple qui soit et on appelle cette fraction continue \(\varphi\). \[\varphi = 1 + \cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\dots}}}\]En soustrayant \(1\) de chaque côté, on obtient\[\varphi-1 = \cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+ \dots}}}\]Puis en inversant \[\frac{1}{\varphi-1}=\frac{1+\cfrac{1}{1+\cfrac{1}{1+\dots}}}{1}\]ce qui n’est rien d’autre que \[\frac{1}{\varphi-1}=\frac{\varphi}{1}\]La fraction continue du départ est donc égale au nombre d’or, la solution positive de l’équation \[\varphi^{2}-\varphi-1=0\]Nous connaissons cette valeur grâce à la formule quadratique ou la complétion du carré. C’est \[\varphi=\frac{1+\sqrt{5}}{2}\] et d’où l’on tire \[\frac{1+\sqrt{5}}{2}=1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\dots}}}}\]Ceci étant dit, lorsqu’on calcule les réduites de la fraction continue simple, on obtient \begin{align*}1+\cfrac{1}{1}=1+1&=\frac{2}{1} \\ \\ 1+\cfrac{1}{1+\frac{1}{1}}=1+\frac{1}{2}&=\frac{3}{2} \\ \\ 1+\cfrac{1}{1+\cfrac{1}{1+\frac{1}{1}}}=1+\cfrac{1}{1+\frac{1}{2}} = 1 +\frac{1}{\frac{3}{2}} &= \frac{5}{3} \\ \\ 1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\frac{1}{1}}}}=1+\cfrac{1}{1+\cfrac{1}{1+\frac{1}{2}}}=1+\cfrac{1}{1+\frac{3}{2}}=1+\cfrac{1}{\frac{5}{3}}&=\frac{8}{5} \\ \\ 1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\frac{1}{1}}}}}= \ \dots \ = 1+\frac{1}{\frac{8}{5}}&=\frac{13}{8}\\ \\ 1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\frac{1}{1}}}}}} = \ \dots \ &= \frac{21}{13} \\ \\ &\dots\end{align*}On obtient les rapports successifs des termes consécutifs de la suite de Fibonacci ! Ces rapports tendent donc vers le nombre d’or ! On écriera donc \begin{align*}u_{1}&=1 \\ \\ u_{2}&=1 \\ \\ u_{n}&=u_{n-1}+u_{n-2} \\ \\ \\ \varphi &= \lim_{n\to \infty}\frac{u_{n+1}}{u_{n}}\end{align*}Nous reviendrons à ce résultat exceptionnel plus tard. Il existe une formule qui nous permet d’exprimer directement le \(n\)^ième terme de la suite de Fibonacci. Cette formule est la suivante \[u_{n} = \frac{1}{\sqrt{5}}\left(\varphi^{n}-\left(1-\varphi\right)^{n}\right)\]Il n’est donc pas surprenant d’y retrouver le nombre d’or. Les techniques pour trouver cette formule directement étant un peu avancées, nous nous contenterons d’en fournir la preuve par induction. Commençons d’abord par vérifier qu’elle soit vraie pour les premières valeurs de \(n\). En se rappelant que \[\varphi = \frac{1+\sqrt{5}}{2}\]on peut trouver que\begin{align*}u_{1}&=\frac{1}{\sqrt{5}}\left(\varphi^{1}-(1-\varphi)^{1}\right)\\  \\ &=\frac{2\varphi-1}{\sqrt{5}} \\ \\ &=\frac{1+\sqrt{5}-1}{\sqrt{5}} \\ \\ &=1\end{align*} et \begin{align*}u_{2}&=\frac{1}{\sqrt{5}}\left(\varphi^{2}-(1-\varphi)^{2}\right)\\  \\ &=\frac{\varphi^{2}-(1-2\varphi + \varphi^{2})}{\sqrt{5}} \\ \\ &=\frac{2\varphi-1}{\sqrt{5}}\\ \\ &=\frac{1+\sqrt{5}-1}{\sqrt{5}} \\ \\ &=1\end{align*}La formule fonctionne donc pour les premières valeurs de \(n\). Supposons alors qu’elle soit vraie pour tout entier \(k\) tel que \[1\leq k \leq n\]C’est notre hypothèse d’induction. Montrons qu’elle sera aussi vraie pour \(n+1\). On sait que \[u_{n+1}=u_{n}+u_{n-1}\]et comme la formule est valide, par hypothèse, pour tout entier \(k\) jusqu’à \(n\) (cela inclut, au passage, \(n-1\) et, incidemment, nous avions vérifié deux termes au départ, et non pas un seul), on peut réécrire \[u_{n+1}=\frac{1}{\sqrt{5}}\left(\varphi^{n}-\left(1-\varphi\right)^{n}\right)+\frac{1}{\sqrt{5}}\left(\varphi^{n-1}-\left(1-\varphi\right)^{n-1}\right)\]Un mise en évidence fait \[u_{n+1}=\frac{1}{\sqrt{5}}\left(\varphi^{n}-\left(1-\varphi\right)^{n}+\varphi^{n-1}-\left(1-\varphi\right)^{n-1}\right)\]puis en réarrangeant les termes \[u_{n+1}=\frac{1}{\sqrt{5}}\left(\varphi^{n}+\varphi^{n-1}-\left(\left(1-\varphi\right)^{n}+\left(1-\varphi\right)^{n-1}\right)\right)\]Une double mise en évidence nous permet d’écrire \[u_{n+1}=\frac{1}{\sqrt{5}}=\left(\varphi^{n}\left(1+\varphi^{-1}\right)-\left(1-\varphi\right)^{n}\left(1+\left(1-\varphi\right)^{-1}\right)\right)\]Or, comme \[\varphi = 1+\varphi^{-1}\]puisque \begin{align*}1+\varphi^{-1}&=1+\frac{2}{1+\sqrt{5}} \\ \\ &=\frac{1+\sqrt{5}+2}{1+\sqrt{5}} \\ \\ &=\frac{3+\sqrt{5}}{1+\sqrt{5}} \\ \\ &= \frac{3+\sqrt{5}}{1+\sqrt{5}} \cdot \frac{1-\sqrt{5}}{1-\sqrt{5}}\\ \\ &=\frac{3-3\sqrt{5}+\sqrt{5}-5}{1-5} \\ \\ &= \frac{-2-2\sqrt{5}}{-4} \\ \\ &=\frac{1+\sqrt{5}}{2} \\ \\ &=\varphi\end{align*}et \[1-\varphi = 1 +\left(1-\varphi\right)^{-1}\]puisque \begin{align*}1+\left(1-\varphi\right)^{-1}&=1+\left(\frac{1-\sqrt{5}}{2}\right)^{-1} \\ \\ &=1+\frac{2}{1-\sqrt{5}} \\ \\ &=\frac{1-\sqrt{5}+2}{1-\sqrt{5}} \\ \\ &=\frac{3-\sqrt{5}}{1-\sqrt{5}} \\ \\ &=\frac{3-\sqrt{5}}{1-\sqrt{5}} \cdot \frac{1+\sqrt{5}}{1+\sqrt{5}} \\ \\ &=\frac{3+3\sqrt{5}-\sqrt{5}-5}{1-5} \\ \\ &=\frac{-2+2\sqrt{5}}{-4}\\ \\ &=\frac{1-\sqrt{5}}{2} \\ \\ &=1-\varphi\end{align*}il nous suffit de remplacer \[u_{n+1}=\frac{1}{\sqrt{5}}\left(\varphi^{n}\left(\varphi\right)-\left(1-\varphi\right)^{n}\left(1-\varphi\right)\right)\]afin d’obtenir \[u_{n+1}=\frac{1}{\sqrt{5}}\left(\varphi^{n+1}-\left(1-\varphi\right)^{n+1}\right)\]Voilà ! Par le principe d’induction, nous avons prouvé la formule. C’est le mathématicien écossais Robert Simson qui remarqua que \[\lim_{n\to \infty}\frac{u_{n+1}}{u_{n}}=\lim_{n\to \infty}\frac{\frac{1}{\sqrt{5}}\left(\varphi^{n+1}-\left(1-\varphi\right)^{n+1}\right)}{\frac{1}{\sqrt{5}}\left(\varphi^{n}-\left(1-\varphi\right)^{n}\right)}\]Après une première simplification\[\lim_{n\to \infty}\frac{u_{n+1}}{u_{n}}=\lim_{n\to \infty}\frac{\varphi^{n+1}-\left(1-\varphi\right)^{n+1}}{\varphi^{n}-\left(1-\varphi\right)^{n}}\]on effectue deux mises en évidence : l’une au numérateur et l’autre au dénominateur \[\lim_{n\to \infty}\frac{u_{n+1}}{u_{n}}=\lim_{n\to \infty}\frac{\varphi^{n+1}\left(1-\left(\frac{1-\varphi}{\varphi}\right)^{n+1}\right)}{\varphi^{n}\left(1-\left(\frac{1-\varphi}{\varphi}\right)^{n}\right)}\]ce qui fait\[\lim_{n\to \infty}\frac{u_{n+1}}{u_{n}}=\lim_{n\to \infty}\varphi \cdot \frac{1-\left(\frac{1-\varphi}{\varphi}\right)^{n+1}}{1-\left(\frac{1-\varphi}{\varphi}\right)^{n}}\]Or il est facile de voir que si \[1<\varphi<2\]alors \[-1<\frac{1-\varphi}{\varphi}<1\]et cela implique que \[\lim_{n\to \infty}\left(\frac{1-\varphi}{\varphi}\right)^{n}=0\]et évidemment aussi que \[\lim_{n \to \infty}\left(\frac{1-\varphi}{\varphi}\right)^{n+1}=0\]On obtient donc \[\lim_{n\to \infty}\frac{u_{n+1}}{u_{n}} = \varphi \cdot \frac{1-0}{1-0}\]ce qui fait tout simplement \[\lim_{n\to \infty}\frac{u_{n+1}}{u_{n}}=\varphi\]

Nous avions déjà observé dans ce blog que les sommes des premiers impairs, commençant avec \(1\), donnaient les nombres carrés. \begin{align*}1&=1 \\ \\ 1+3 &=4 \\ \\ 1+3+5 &=9 \\ \\ 1 + 3 + 5 +7 &=16 \\ \\ 1 + 3 + 5 +7 + 9 &=25 \\ \\ 1 + 3 + 5 + 7 + 9 + 11 &= 36 \\ \\ &\dots \end{align*}

Aviez-vous seulement remarqué que si, au lieu repartir chaque somme à \(1\), on utilisait l’entier suivant, on obtenait … \begin{align*}1&=1 \\ \\ 3+5 &=8 \\ \\ 7+9+11 &=27 \\ \\ 13 + 15 + 17 +19 &=64 \\ \\ 21 + 23 + 25 +27 + 29 &=125 \\ \\ 31 + 33 + 35 + 37 + 39 + 41 &= 216 \\ \\ &\dots \end{align*}les nombres cubes.

Les mathématiques sont fascinantes.

Référence : John Conway et Richard K. Guy (1995), The Book of Numbers