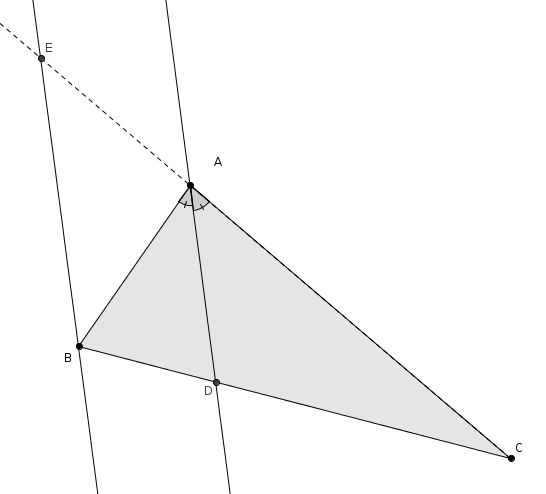
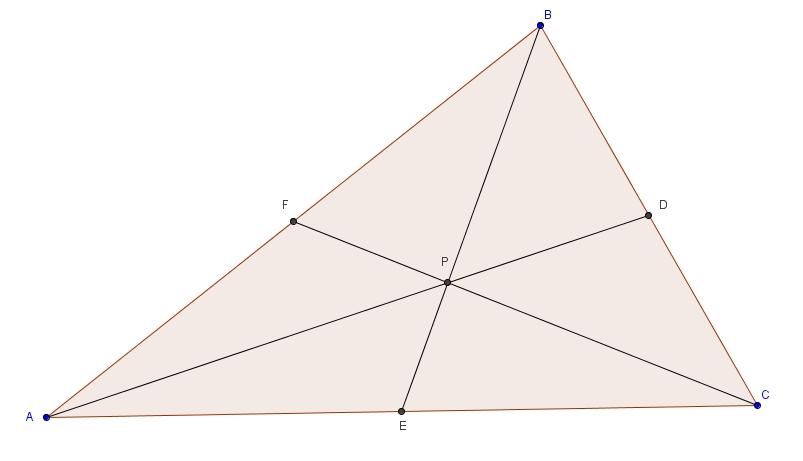
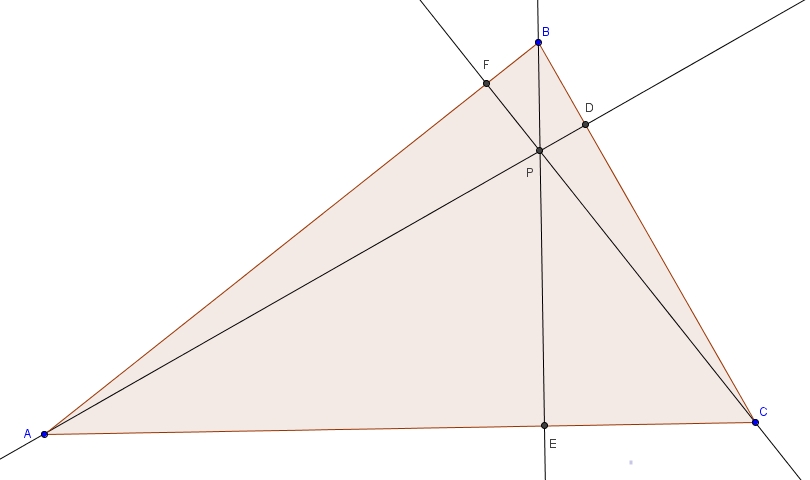
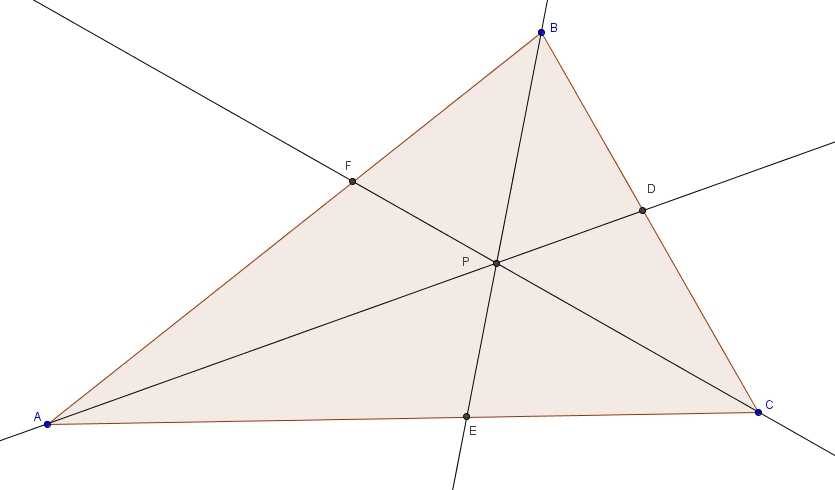
Dans le dernier billet, je mentionnais sans démonstration que dans un triangle, la bissectrice d’un angle divise toujours le côté opposé dans le même rapport que les côtés de l’angle. Considérons le triangle \(ABC\) suivant, avec la bissectrice de l’angle \(A\) qui coupe \(\overline{BC}\) en \(D\). Il suffit de tracer l’unique parallèle à \(AD\) passant par \(B\). Prolongeons \(\overline{AC}\) de telle sorte qu’il coupe la parallèle en \(E\).
Les angles \(ADC\) et \(EBC\) sont des angles correspondants isométriques formés par des parallèles (sécante \(BC\)). Les triangles \(EBC\) est \(ADC\) partagent tous les deux l’angle \(DCA\). Les triangles sont donc semblables par le cas de similitude AA. On tire la proportion suivante \[\frac{m\overline{EC}}{m\overline{AC}} = \frac{m\overline{BC}}{m\overline{DC}}\]que l’on peut réécrire de telle façon \[\frac{m\overline{EA}+m\overline{AC}}{m\overline{AC}} = \frac{m\overline{BD}+m\overline{DC}}{m\overline{DC}}\]et donc \[\frac{m\overline{EA}}{m\overline{AC}} + \frac{m\overline{AC}}{m\overline{AC}} = \frac{m\overline{BD}}{m\overline{DC}} + \frac{m\overline{DC}}{m\overline{DC}}\]ce qui fait \[\frac{m\overline{EA}}{m\overline{AC}}+1 = \frac{m\overline{BD}}{m\overline{DC}}+1\]Enfin en soustrayant \(1\) de chaque côté de l’égalité on obtient \[\frac{m\overline{EA}}{m\overline{AC}} = \frac{m\overline{BD}}{m\overline{DC}}\]Les angles \(BAD\) et \(CAD\) sont isométriques puisque \(AD\) est la bissectrice. Les angles \(BAD\) et \(ABE\) sont isométriques puisque ce sont des angles alternes-internes formés par des parallèles (la sécante étant \(AB\)). Enfin, les angles \(AEB\) et \(CAD\) sont isométriques puisque ce sont des angles correspondants formés par des parallèles (la sécante ici étant \(AE\)). Par transitivité, on trouve que les angles \(DAC\), \(BAD\), \(ABE\) et \(AEB\) sont tous isométriques. Cela implique que le triangle \(EAB\) est un triangle isoangle. Les triangles isoangles étant isocèles, et dans ces triangles les angles opposés aux côtés isométriques étant isométriques, on a \[ \overline{EA}\cong \overline{AB}\]La proportion \[\frac{m\overline{EA}}{m\overline{AC}} = \frac{m\overline{BD}}{m\overline{DC}}\]devient \[\frac{m\overline{AB}}{m\overline{AC}} = \frac{m\overline{BD}}{m\overline{DC}}\]ou de façon équivalente \[\frac{m\overline{AB}}{m\overline{BD}} = \frac{m\overline{AC}}{m\overline{DC}}\]ce que l’on cherchait à démontrer !
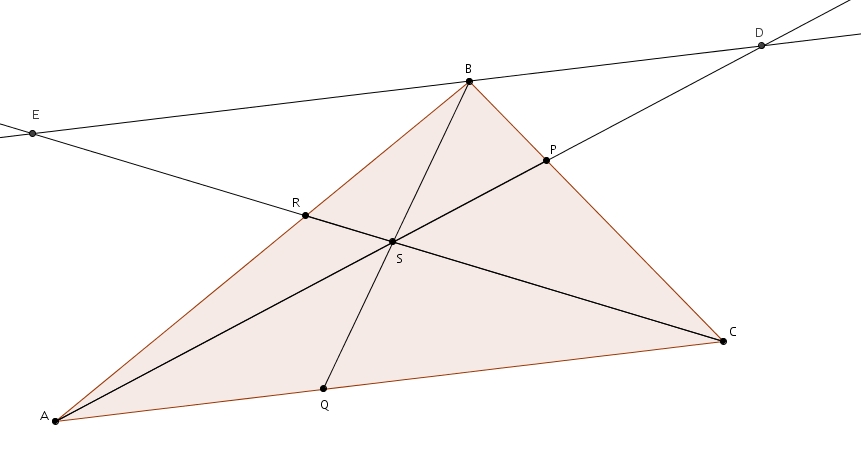
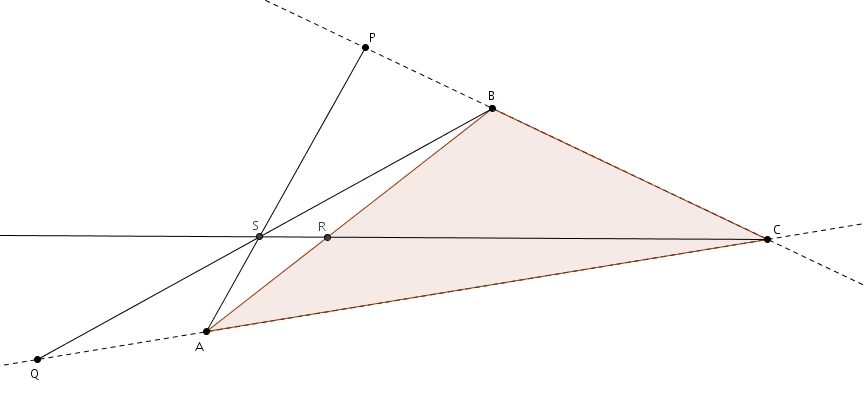
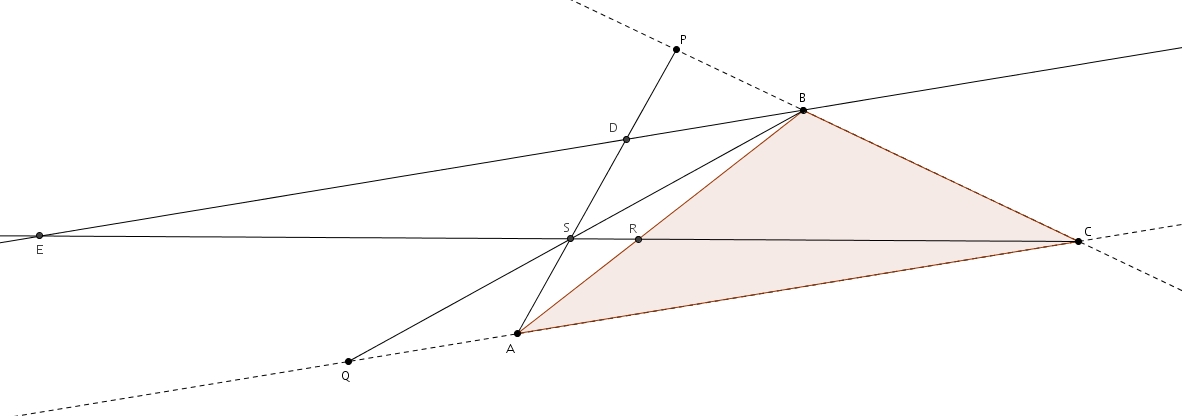
La preuve tient aussi de façon presque intégrale lorsqu’on considère la bissectrice de l’angle extérieur, bien que le résultat peut paraître surprenant, de prime abord. En reprenant le triangle \(ABC\) et en considérant la bissectrice extérieure à l’angle \(A\) on a
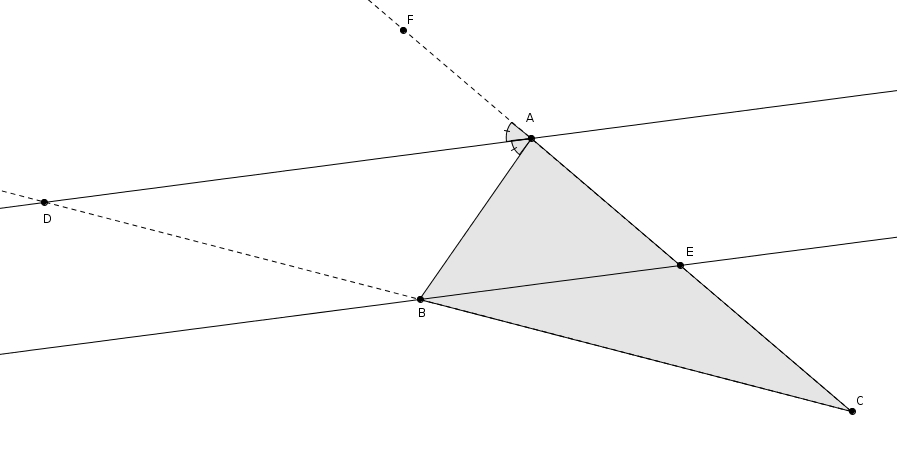 La bissectrice coupe le prolongement du côté \(BC\) en \(D\). On trace la parallèle à la bissectrice passant par \(B\) et coupant \(\overline{AC}\) en \(E\). Les angles \(CEB\) et \(CAD\) sont isométriques puisque ce sont des angles correspondants formés par des parallèles (la sécante est \(AE\)). Les triangles \(CAD\) et \(CEB\) sont semblables par le cas AA puisqu’ils partagent aussi l’angle \(BCE\). On tire donc la proportion suivante \[\frac{m\overline{EC}}{m\overline{AC}} = \frac{m\overline{BC}}{m\overline{DC}}\]que l’on peut réécrire comme \[\frac{m\overline{AC}-m\overline{AE}}{m\overline{AC}} = \frac{m\overline{DC}-m\overline{DB}}{m\overline{DC}}\]puis \[\frac{m\overline{AC}}{m\overline{AC}}-\frac{m\overline{AE}}{m\overline{AC}}=\frac{m\overline{DC}}{m\overline{DC}}-\frac{m\overline{DB}}{m\overline{DC}}\]ce qui fait \[\frac{m\overline{AE}}{m\overline{AC}} = \frac{m\overline{DB}}{m\overline{DC}}\]Puisqu’il s’agit de la bissectrice \(AD\), les angles \(DAF\) et \(DAB\) sont isométriques. Les angles \(DAB\) et \(ABE\) sont aussi isométriques puisque ce sont des angles alternes-internes formés par des parallèles (la sécante est \(AB\)). Les angles \(DAF\) et \(AEB\) sont aussi isométriques puisque ce sont des angles correspondants formés par des parallèles (la sécante est \(AE\)). Par transitivité les angles \(DAF\), \(DAB\), \(ABE\) et \(AEB\) sont isométriques. Le triangle \(ABE\) est donc un triangle isoangle et isocèle.
La bissectrice coupe le prolongement du côté \(BC\) en \(D\). On trace la parallèle à la bissectrice passant par \(B\) et coupant \(\overline{AC}\) en \(E\). Les angles \(CEB\) et \(CAD\) sont isométriques puisque ce sont des angles correspondants formés par des parallèles (la sécante est \(AE\)). Les triangles \(CAD\) et \(CEB\) sont semblables par le cas AA puisqu’ils partagent aussi l’angle \(BCE\). On tire donc la proportion suivante \[\frac{m\overline{EC}}{m\overline{AC}} = \frac{m\overline{BC}}{m\overline{DC}}\]que l’on peut réécrire comme \[\frac{m\overline{AC}-m\overline{AE}}{m\overline{AC}} = \frac{m\overline{DC}-m\overline{DB}}{m\overline{DC}}\]puis \[\frac{m\overline{AC}}{m\overline{AC}}-\frac{m\overline{AE}}{m\overline{AC}}=\frac{m\overline{DC}}{m\overline{DC}}-\frac{m\overline{DB}}{m\overline{DC}}\]ce qui fait \[\frac{m\overline{AE}}{m\overline{AC}} = \frac{m\overline{DB}}{m\overline{DC}}\]Puisqu’il s’agit de la bissectrice \(AD\), les angles \(DAF\) et \(DAB\) sont isométriques. Les angles \(DAB\) et \(ABE\) sont aussi isométriques puisque ce sont des angles alternes-internes formés par des parallèles (la sécante est \(AB\)). Les angles \(DAF\) et \(AEB\) sont aussi isométriques puisque ce sont des angles correspondants formés par des parallèles (la sécante est \(AE\)). Par transitivité les angles \(DAF\), \(DAB\), \(ABE\) et \(AEB\) sont isométriques. Le triangle \(ABE\) est donc un triangle isoangle et isocèle.
Dans un triangle isocèle les angles opposés aux côtés isométriques sont isométriques et alors on a \[\overline{AE}\cong \overline{AB}\]La proportion \[\frac{m\overline{AE}}{m\overline{AC}} = \frac{m\overline{DB}}{m\overline{DC}}\]devient \[\frac{m\overline{AB}}{m\overline{AC}} = \frac{m\overline{DB}}{m\overline{DC}}\]ou de façon équivalente \[\frac{m\overline{AB}}{m\overline{DB}}=\frac{m\overline{AC}}{m\overline{DC}}\]ce que l’on cherchait à démontrer !