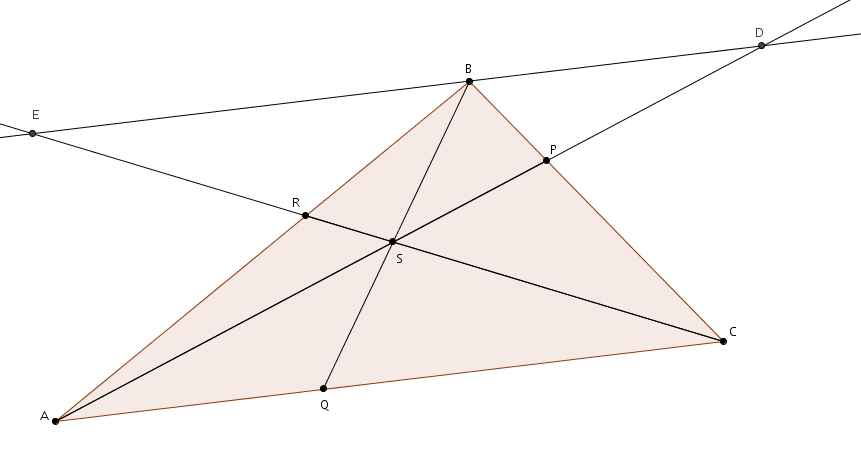
Le théorème de Ceva

Le théorème de Ceva concerne les segments reliant sommets et côtés opposés dans les triangles.

Le théorème de Ceva…

Considérons le triangle 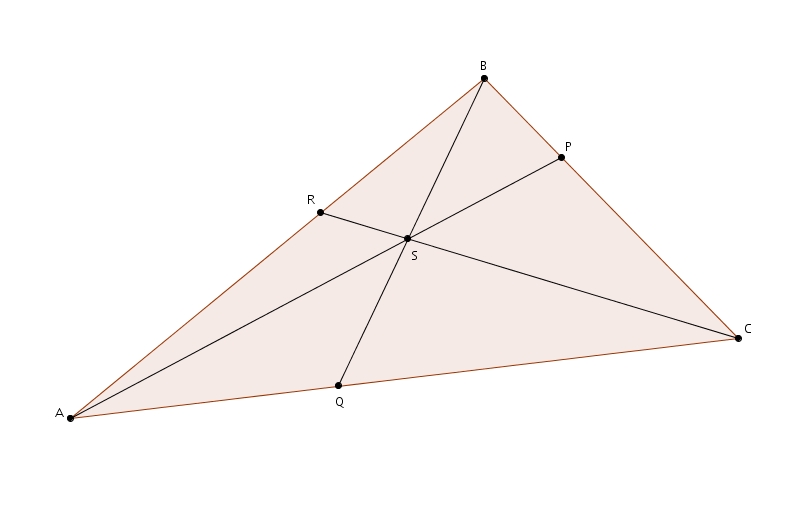$ABC$ suivant.

Plaçons $P$ sur $\overline{BC}$, $Q$ sur $\overline{AC}$ et $R$ sur $\overline{AB}$.  Les segments $AP$, $BQ$ et $CR$ se rencontrent en $S$ si et seulement si $$\frac{m\overline{AR}}{m\overline{RB}}\cdot \frac{m\overline{BP}}{m\overline{PC}}\cdot \frac{m\overline{CQ}}{m\overline{QA}}=1$$Il existe plusieurs démonstrations différentes de ce résultat.  Traçons l’unique parallèle à $AC$ passant par $B$.  Prolongeons les segments $AP$ et $CR$ de telle sorte qu’ils coupent la parallèle respectivement en $D$ et $E$.  Nous avons à notre disposition une armée de triangles semblables.  Il suffit de choisir les bonnes combinaisons.

• 1. Les angles $BDP$ et $CAP$ sont des angles alternes-internes isométriques formés par des parallèles.  Les angles $APC$ et $DPB$ sont isométriques puisqu’ils sont opposés par le sommet.  Les triangles $APC$ et $DPB$ sont donc semblables par le cas de similitude AA.  Grâce à cette similitude, on tire la proportion suivante $$\frac{m\overline{BP}}{m\overline{PC}}=\frac{m\overline{BD}}{m\overline{CA}}$$
• 2. Les angles $RCA$ et $REB$  sont des angles alternes-internes isométriques formés par des parallèles.  Les angles $CRA$ et $ERB$ sont isométriques puisqu’ils sont opposés par le sommet.  Les triangles $CRA$ et $ERB$ sont donc semblables par le cas de similitude AA.  Grâce à cette similitude, on tire la proportion suivante $$\frac{m\overline{AR}}{m\overline{RB}}=\frac{m\overline{CA}}{m\overline{EB}}$$
• 3. Les angles $SCQ$ et $SEB$  sont des angles alternes-internes isométriques formés par des parallèles (déjà montré).  Les angles $QSC$ et $BSE$ sont isométriques puisqu’ils sont opposés par le sommet.  Les triangles $QSC$ et $BSE$ sont donc semblables par le cas de similitude AA.  Grâce à cette similitude, on tire la proportion suivante $$\frac{m\overline{CQ}}{m\overline{EB}}=\frac{m\overline{QS}}{m\overline{BS}}$$
• 4. Enfin, les angles $SAQ$ et $SDB$  sont des angles alternes-internes isométriques formés par des parallèles (déjà montré).  Les angles $ASQ$ et $DSB$ sont isométriques puisqu’ils sont opposés par le sommet.  Les triangles $ASQ$ et $DSB$ sont donc semblables par le cas de similitude AA.  Grâce à cette similitude, on tire la proportion suivante $$\frac{m\overline{AQ}}{m\overline{DB}}=\frac{m\overline{QS}}{m\overline{BS}}$$

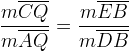Grâce à 3 et 4, on tire $$\frac{m\overline{CQ}}{m\overline{EB}}=\frac{m\overline{AQ}}{m\overline{DB}}$$qu’on peut aussi écrire comme $$\frac{m\overline{CQ}}{m\overline{AQ}}=\frac{m\overline{EB}}{m\overline{DB}}$$En multipliant les trois rapports $$\frac{m\overline{BP}}{m\overline{PC}}\cdot \frac{m\overline{AR}}{m\overline{RB}}\cdot \frac{m\overline{CQ}}{m\overline{AQ}}$$et en utilisant le dernier résultat ainsi que les résultats 1 et 2, on obtient $$\frac{m\overline{BD}}{m\overline{CA}}\cdot \frac{m\overline{CA}}{m\overline{EB}}\cdot \frac{m\overline{EB}}{m\overline{BD}}=1$$ce qui nous permet d’écrire finalement $$\frac{m\overline{AR}}{m\overline{RB}}\cdot \frac{m\overline{BP}}{m\overline{PC}}\cdot \frac{m\overline{CQ}}{m\overline{QA}}=1$$Il reste à fournir la preuve de la réciproque.

… et sa réciproque

Supposons que les segments $AP$ et $BQ$ se rencontrent en $S$ et plaçons $R$ sur $\overline{AB}$ de telle sorte que $$\frac{m\overline{AR}}{m\overline{RB}}\cdot \frac{m\overline{BP}}{m\overline{PC}}\cdot \frac{m\overline{CQ}}{m\overline{QA}}=1$$Traçons $\overline{CS}$ et prolongeons $\overline{CS}$ jusqu’à $\overline{AB}$.  $CS$ coupe $\overline{AB}$ en $R^{\prime }$.

Or, si les segments $AP$, $BQ$ et $C{R}^{\prime }$ sont concourants, alors, par le Théorème de Ceva (celui-là même que l’on vient de prouver), on trouve $$\frac{m\overline{A{R}^{\prime }}}{m\overline{R^{\prime }B}}\cdot \frac{m\overline{BP}}{m\overline{PC}}\cdot \frac{m\overline{CQ}}{m\overline{QA}}=1$$Cependant, en rappelant notre hypothèse, $$\frac{m\overline{AR}}{m\overline{RB}}\cdot \frac{m\overline{BP}}{m\overline{PC}}\cdot \frac{m\overline{CQ}}{m\overline{QA}}=1$$cela implique que $$\frac{m\overline{A{R}^{\prime }}}{m\overline{R^{\prime }B}}=\frac{m\overline{AR}}{m\overline{RB}}$$Et en additionnant $1$ de chaque côté… $$\frac{m\overline{A{R}^{\prime }}}{m\overline{R^{\prime }B}}+1=\frac{m\overline{AR}}{m\overline{RB}}+1$$on obtient $$\frac{m\overline{A{R}^{\prime }}}{m\overline{R^{\prime }B}}+\frac{m\overline{R^{\prime }B}}{m\overline{R^{\prime }B}}=\frac{m\overline{AR}}{m\overline{RB}}+\frac{m\overline{RB}}{m\overline{RB}}$$et donc $$\frac{m\overline{A{R}^{\prime }}+m\overline{R^{\prime }B}}{m\overline{R^{\prime }B}}=\frac{m\overline{AR}+m\overline{RB}}{m\overline{RB}}$$On peut réécrire les numérateurs $$\frac{m\overline{AB}}{m\overline{R^{\prime }B}}=\frac{m\overline{AB}}{m\overline{RB}}$$afin de conclure $$m\overline{R^{\prime }B}=m\overline{RB}$$c’est-à dire que $R^{\prime }$ et $R$ sont confondus.  La réciproque est prouvée.

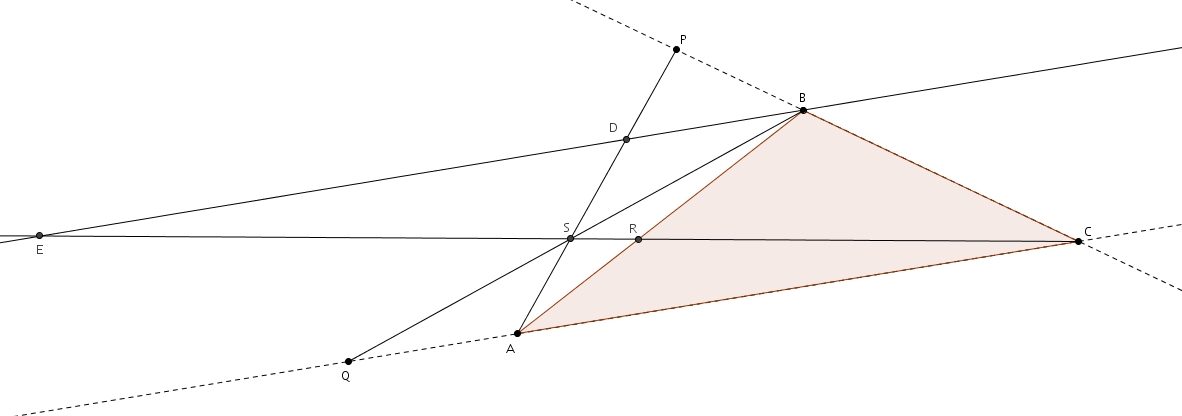
Les points $P$, $Q$ et $R$ ne sont pas nécessairement sur les côtés du triangles : ils peuvent se trouver sur les prolongements des côtés, tel qu’illustré dans le figure suivante :

On trace la parallèle à $AC$ passant par $B$ de la même façon afin d’obtenir

Tout le raisonnement ci-haut reste valide.

Le théorème de Ceva peut se trouver très utile lorsque vient le temps de fournir la preuve que des segments dans un triangle se rencontrent en un point.  Dans ce billet et ce celui-ci on prouve que les médianes, les hauteurs et les bissectrices d’un triangle sont concourantes.  Nous allons revisiter ces preuves avec le théorème de Ceva.  Il s’avère que le travail sera beaucoup moins fastidieux.

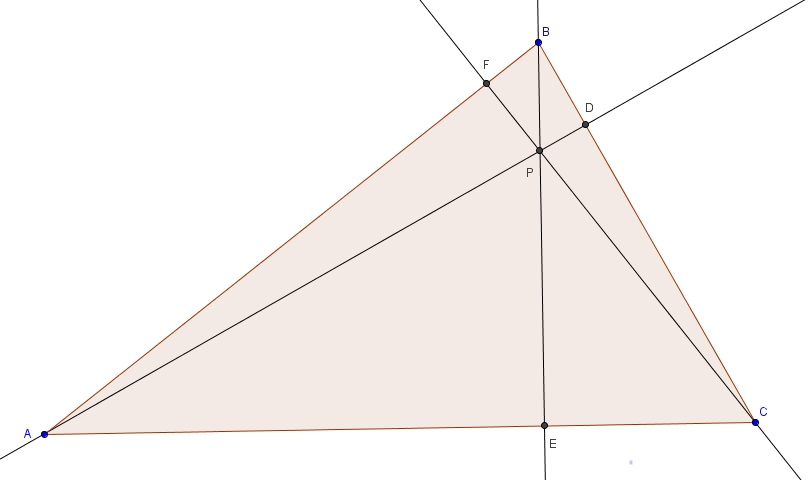
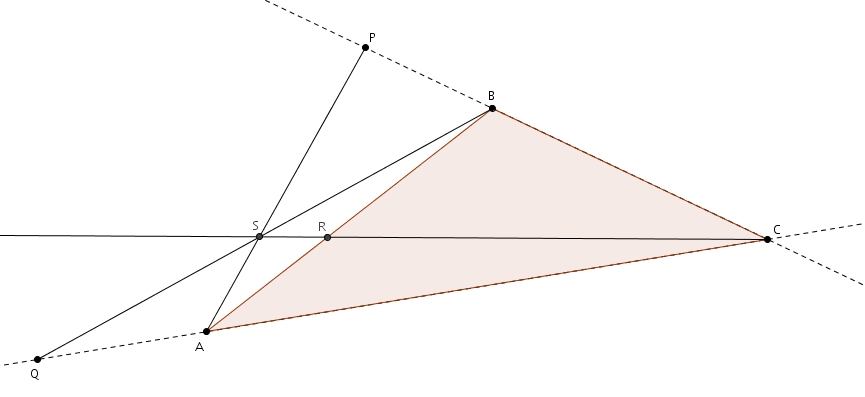
Les médianes

Dans un triangle $ABC$, on trace les médianes $AD$, $BE$ et $CF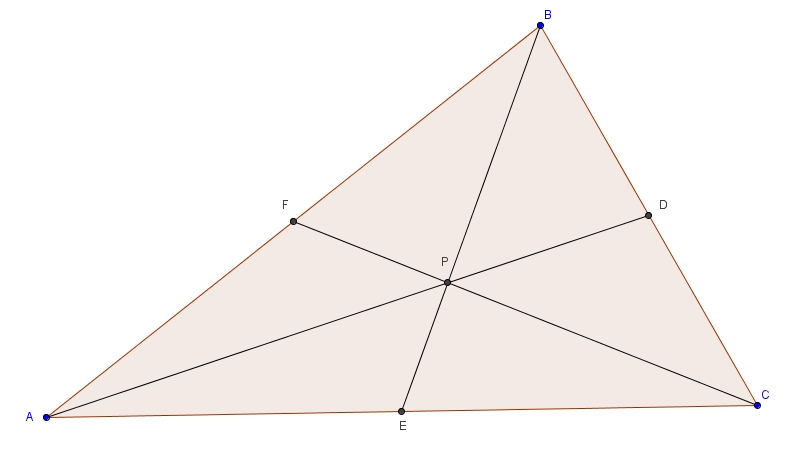$. Par définition même de médiane, on sait que $$m\overline{AF}=m\overline{FB},m\overline{BD}=m\overline{DC},m\overline{CE}=m\overline{EA}$$Il va sans dire que l’on trouve facilement $$\frac{m\overline{AF}}{m\overline{FB}}\cdot \frac{m\overline{BD}}{m\overline{DC}}\cdot \frac{m\overline{CE}}{m\overline{EA}}=1$$et par le Théorème de Ceva, on peut affirmer que les médianes sont concourantes en $P$.

Les hauteurs

Dans le triangle $ABC$, on trace les hauteurs $AD$, $BE$ et $CF$.

Les triangles $BFC$ et $ADB$ sont tous deux rectangles et partagent l’angle $FBD$.  On peut donc affirmer qu’ils sont semblables par le cas de similitude AA.  On tire cette proportion $$\frac{m\overline{BF}}{m\overline{DB}}=\frac{m\overline{BC}}{m\overline{BA}}$$Les triangles $AEB$ et $AFC$ sont tous deux rectangles et partagent l’angle $FAE$.  On peut donc affirmer qu’ils sont semblables par le cas de similitude AA.  On tire cette proportion $$\frac{m\overline{AE}}{m\overline{FA}}=\frac{m\overline{BA}}{m\overline{AC}}$$Les triangles $CDA$ et $CEB$ sont tous deux rectangles et partagent l’angle $DCE$.  On peut donc affirmer qu’ils sont semblables par le cas de similitude AA.  On tire cette proportion $$\frac{m\overline{CD}}{m\overline{EC}}=\frac{m\overline{AC}}{m\overline{BC}}$$Il suffit de multiplier ces trois égalités afin d’obtenir $$\frac{m\overline{BF}}{m\overline{DB}}\cdot \frac{m\overline{AE}}{m\overline{FA}}\cdot \frac{m\overline{CD}}{m\overline{EC}}=\frac{m\overline{BC}}{m\overline{BA}}\cdot \frac{m\overline{BA}}{m\overline{AC}}\cdot \frac{m\overline{AC}}{m\overline{BC}}=1$$Par le théorème de Ceva, on est en mesure d’affirmer que les hauteurs sont concourantes en $P$.

Les bissectrices

Dans le triangle $ABC$, on trace les bissectrices $AD$, $BE$, $CF$.

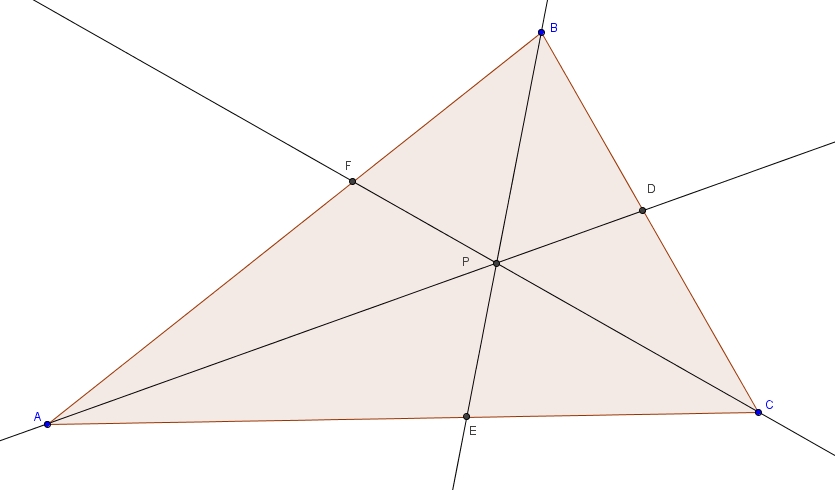Dans un triangle, les bissectrices divisent toujours le côté opposé en deux segments proportionnels aux côtés de l’angle.  Il suffit donc de tirer, avec, respectivement, les bissectrices $CF$, $AD$ et $BE$, $$\frac{m\overline{AF}}{m\overline{FB}}=\frac{m\overline{AC}}{m\overline{BC}},\frac{m\overline{BD}}{m\overline{DC}}=\frac{m\overline{AB}}{m\overline{AC}},\frac{m\overline{CE}}{m\overline{EA}}=\frac{m\overline{BC}}{m\overline{AB}}$$et donc en multipliant $$\frac{m\overline{AF}}{m\overline{FB}}\cdot \frac{m\overline{BD}}{m\overline{DC}}\cdot \frac{m\overline{CE}}{m\overline{EA}}=\frac{m\overline{AC}}{m\overline{BC}}\cdot \frac{m\overline{AB}}{m\overline{AC}}\cdot \frac{m\overline{BC}}{m\overline{AB}}=1$$Par le théorème de Ceva, on peut donc affirmer que les trois bissectrices sont concourantes en $P$.

Référence :  Alfred S. Posamentier et  Charles T. Salkind (1996), Challenging Problems In Geometry