Parmi les quelques notions évacuées dans le nouveau programme de quatrième secondaire, on retrouve la formule de la distance entre un point et une droite. Cela me semble bienvenu puisque je ne connaissais pas beaucoup d’enseignants prêts à en fournir une démonstration en classe, et encore moins d’élèves pour la suivre. En voici une.
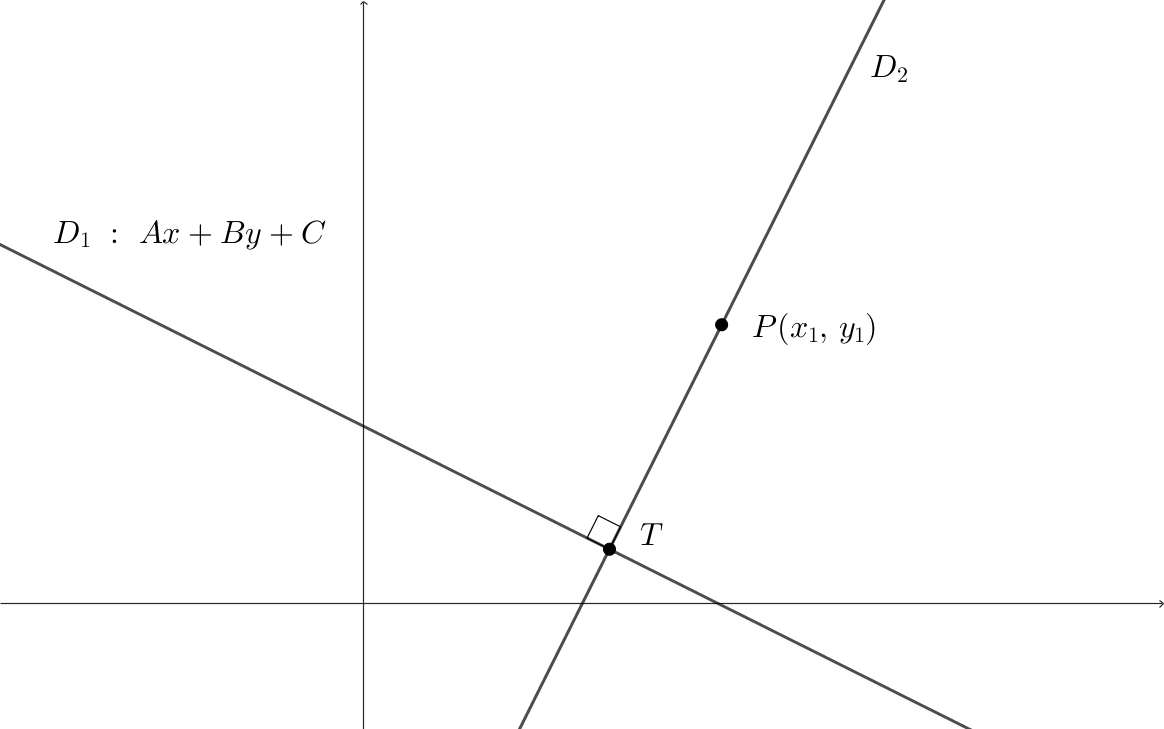
Considérons la droite \[D_{1}\ : \ Ax + By + C = 0 \]et le point \[P(x_{1}, \, y_{1})\](hors de la droite) dans le plan (ici, habituellement, \(A\), \(B\) et \(C\) sont des entiers et \(A\) est positif).

On cherche la distance entre le point et la droite. Cette distance est la mesure du segment perpendiculaire à la droite \(D_{1}\) passant par \(P\). Traçons donc la droite \(D_{2}\), perpendiculaire à la droite \(D_{1}\) et passant par \(P\), sécante en \(T\), telle que
On peut d’abord transformer l’équation générale de \(D_{1}\) et trouver son équation fonctionnelle (si \(B\) n’est pas nul). On a d’abord \[-By = Ax + C\]puis en divisant par \(-B\) [1]\[y = -\frac{A}{B}x-\frac{C}{B}\]Si la pente de cette droite est \(-\frac{A}{B}\) alors la pente de \(D_{2}\), perpendiculaire, sera donc l’opposé de l’inverse de la pente de \(D_{1}\), soit \(\frac{B}{A}\) et son équation sera de la forme \[y = \frac{B}{A}x + b\]On peut trouver l’ordonnée à l’origine \(b\) en remplaçant \(x\) et \(y\) par les coordonnées de \(P\) \[y_{1}=\frac{B}{A}x_{1}+b\]et en isolant \(b\) \[y_{1}-\frac{B}{A}x_{1}=b\]ce qui nous permet d’obtenir la forme fonctionnelle de \(D_{2}\) \[y = \frac{B}{A}x + \left(y_{1}-\frac{B}{A}x_{1}\right)\]Il nous est donc possible de comparer les équations sous forme fonctionnelle des deux droites afin de résoudre le système d’équations. Nous obtiendrons de cette façon les coordonnées du point \(T\). \[-\frac{A}{B}x-\frac{C}{B}=\frac{B}{A}x+y_{1}-\frac{B}{A}x_{1}\]Avant quoi que ce soit, cherchons le dénominateur commun \(AB\) \[-\frac{A^{2}}{AB}x-\frac{AC}{AB}=\frac{B^{2}}{AB}x + \frac{ABy_{1}}{AB}-\frac{B^{2}}{AB}x_{1}\]afin d’obtenir \[-A^{2}x-AC=B^{2}x+ABy_{1}-B^{2}x_{1}\]On regroupe par la suite les termes en x d’un côté \[A^{2}x+B^{2}x=B^{2}x_{1}-ABy_{1}-AC\]La mise en évidence de x nous donne \[x\left(A^{2}+B^{2}\right) = B^{2}x_{1}-ABy_{1}-AC\]et donc \[x = \frac{B^{2}x_{1}-ABy_{1}-AC}{A^{2}+B^{2}}\]C’est l’abscisse du point \(T\). Pour trouver l’ordonnée, il faut remplacer cette valeur dans l’une ou l’autre des équations. En choisissant celle de \(D_{1}\) \[y = -\frac{A}{B}x-\frac{C}{B}\]on obtient \[y = -\frac{A}{B}\left(\frac{B^{2}x_{1}-ABy_{1}-AC}{A^{2}+B^{2}}\right)-\frac{C}{B}\]ce qui donne \[y = \frac{-AB^{2}x_{1}+A^{2}By_{1}+A^{2}C}{B\left(A^{2}+B^{2}\right)}-\frac{C}{B}\]puis en mettant sur dénominateur commun \[y = \frac{-AB^{2}x_{1}+A^{2}By_{1}+A^{2}C}{B\left(A^{2}+B^{2}\right)}-\frac{C\left(A^{2}+B^{2}\right)}{B\left(A^{2}+B^{2}\right)}\]et donc \[y = \frac{-AB^{2}x_{1}+A^{2}By_{1}+A^{2}C}{B\left(A^{2}+B^{2}\right)}-\frac{A^{2}C+B^{2}C}{B\left(A^{2}+B^{2}\right)}\]En effectuant la soustraction on obtient \[y = \frac{-AB^{2}x_{1}+A^{2}By_{1}+A^{2}C-A^{2}C-B^{2}C}{B\left(A^{2}+B^{2}\right)}\]puis après simplification de deux des termes \[y = \frac{-AB^{2}x_{1}+A^{2}By_{1}-B^{2}C}{B\left(A^{2}+B^{2}\right)}\]et enfin après la simplification du facteur \(B\) \[y = \frac{-ABx_{1}+A^{2}y_{1}-BC}{A^{2}+B^{2}}\]Les coordonnées de \(T\) sont donc \[\left(\frac{B^{2}x_{1}-ABy_{1}-AC}{A^{2}+B^{2}}, \ \frac{-ABx_{1}+A^{2}y_{1}-BC}{A^{2}+B^{2}}\right)\]Pas simple ! Et cela ne semble pas s’améliorer d’un poil lorsqu’on considère la distance entre \(P\) et \(T\), donnée par \[d(P,\, T) = \sqrt{\left(x_{1}-\frac{B^{2}x_{1}-ABy_{1}-AC}{A^{2}+B^{2}}\right)^{2}+ \left(y_{1}-\frac{-ABx_{1}+A^{2}y_{1}-BC}{A^{2}+B^{2}}\right)^{2}}\]En exprimant les termes dans les parenthèses sous dénominateur commun on obtient \[d(P, \, T) = \sqrt{\left(\frac{x_{1}\left(A^{2}+B^{2}\right)}{A^{2}+B^{2}}-\frac{B^{2}x_{1}-ABy_{1}-AC}{A^{2}+B^{2}}\right)^{2} + \left(\frac{y_{1}\left(A^{2}+B^{2}\right)}{A^{2}+B^{2}}-\frac{-ABx_{1}+A^{2}y_{1}-BC}{A^{2}+B^{2}}\right)^{2}}\]ce qui fait après distribution \[d(P, \, T) = \sqrt{\left(\frac{A^{2}x_{1}+B^{2}x_{1}}{A^{2}+B^{2}}-\frac{B^{2}x_{1}-ABy_{1}-AC}{A^{2}+B^{2}}\right)^{2}+\left(\frac{A^{2}y_{1}+B^{2}y_{1}}{A^{2}+B^{2}}-\frac{-ABx_{1}+A^{2}y_{1}-BC}{A^{2}+B^{2}}\right)^{2}}\]et puis, en effectuant les soustractions \[d(P,\, T) = \sqrt{\left(\frac{A^{2}x_{1}+B^{2}x_{1}-B^{2}x_{1}+ABy_{1}+AC}{A^{2}+B^{2}}\right)^{2}+\left(\frac{A^{2}y_{1}+B^{2}y_{1}+ABx_{1}-A^{2}y_{1}+BC}{A^{2}+B^{2}}\right)^{2}}\]Après une petite simplification de deux termes \[d(P,\, T) = \sqrt{\left(\frac{A^{2}x_{1}+ABy_{1}+AC}{A^{2}+B^{2}}\right)^{2}+\left(\frac{B^{2}y_{1}+ABx_{1}+BC}{A^{2}+B^{2}}\right)^{2}}\]on effectue une double mise en évidence \[d(P, \, T) = \sqrt{\left(\frac{A\left(Ax_{1}+By_{1}+C\right)}{A^{2}+B^{2}}\right)^{2}+\left(\frac{B\left(By_{1}+Ax_{1}+C\right)}{A^{2}+B^{2}}\right)^{2}}\]Une propriété des exposants nous permet d’écrire la dernière expression comme ceci \[d(P, \, T) = \sqrt{\frac{A^{2}\left(Ax_{1}+By_{1}+C\right)^{2}}{\left(A^{2}+B^{2}\right)^{2}}+\frac{B^{2}\left(By_{1}+Ax_{1}+C\right)^{2}}{\left(A^{2}+B^{2}\right)^{2}}}\]Et en effectuant l’addition, on trouve \[d(P,\, T) = \sqrt{\frac{A^{2}\left(Ax_{1}+By_{1}+C\right)^{2}+ B^{2}\left(By_{1}+Ax_{1}+C\right)^{2}}{\left(A^{2}+B^{2}\right)^{2}}}\]Il ne reste qu’à compléter la mise en évidence double \[d(P, \, T) = \sqrt{\frac{\left(Ax_{1}+By_{1}+C\right)^{2}\left(A^{2}+B^{2}\right)}{\left(A^{2}+B^{2}\right)^{2}}}\]et à simplifier \[d(P, \, T) = \sqrt{\frac{\left(Ax_{1}+By_{1}+C\right)^{2}}{A^{2}+B^{2}}}\]Une propriété des racines nous permet d’écrire l’expression précédente comme \[d(P,\, T) = \frac{\sqrt{\left(Ax_{1}+By_{1}+C\right)^{2}}}{\sqrt{A^{2}+B^{2}}}\]ce qui est équivalent à \[d(P, \, T) = \frac{\left| Ax_{1}+By_{1}+C\right|}{\sqrt{A^{2}+B^{2}}}\]Cela nous permet d’écrire enfin \[d(P, \, D_{1}) = \frac{\left|Ax_{1}+By_{1}+C\right|}{\sqrt{A^{2}+B^{2}}}\]Voilà !
[1] Cela implique que \(B \neq 0\). Si \(B=0\), la droite est verticale. Son équation est \[Ax + 0\cdot y + C = 0\]ce qui fait \[Ax + C=0\] et donc \[x = -\frac{A}{C}\]Dans ce cas, la distance entre \(P(x_{0}, \, y_{0})\) et la droite \[D_{1}\ : \ Ax + C = 0\] correspond à l’écart entre les abscisses. Il suffit de constater que la formule fonctionne (en se rappelant que \(A\) est positif)\begin{align*}d(P, D_{1}) &= \frac{\left|Ax_{1}+0\cdot y_{1}+C\right|}{\sqrt{A^{2}+0^{2}}} \\ \\ &=\frac{\left|Ax_{1}+C\right|}{\sqrt{A^{2}}} \\ \\ &= \frac{\left|Ax_{0}+C\right| }{A} \\ \\ &= \left|\frac{Ax_{0}}{A}+\frac{C}{A}\right| \\ \\ &=\left|x_{0}+\frac{C}{A}\right| \\ \\ &= \left|x_{0}-\left(-\frac{C}{A}\right)\right|\end{align*}ce qui est bien l’écart entre les abscisses.
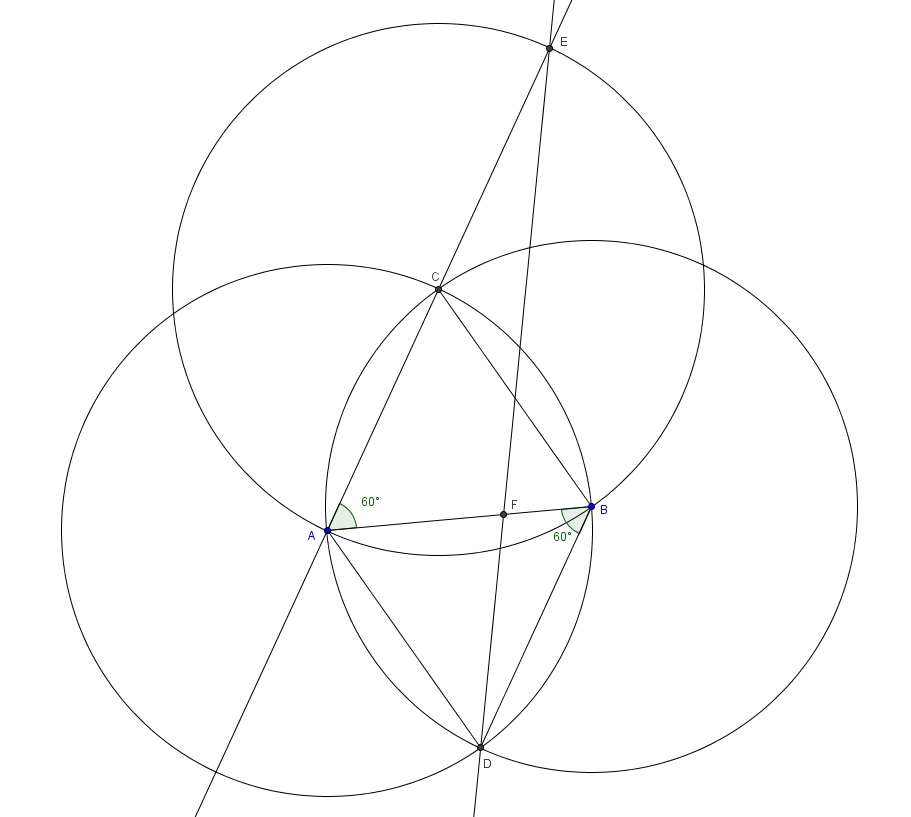
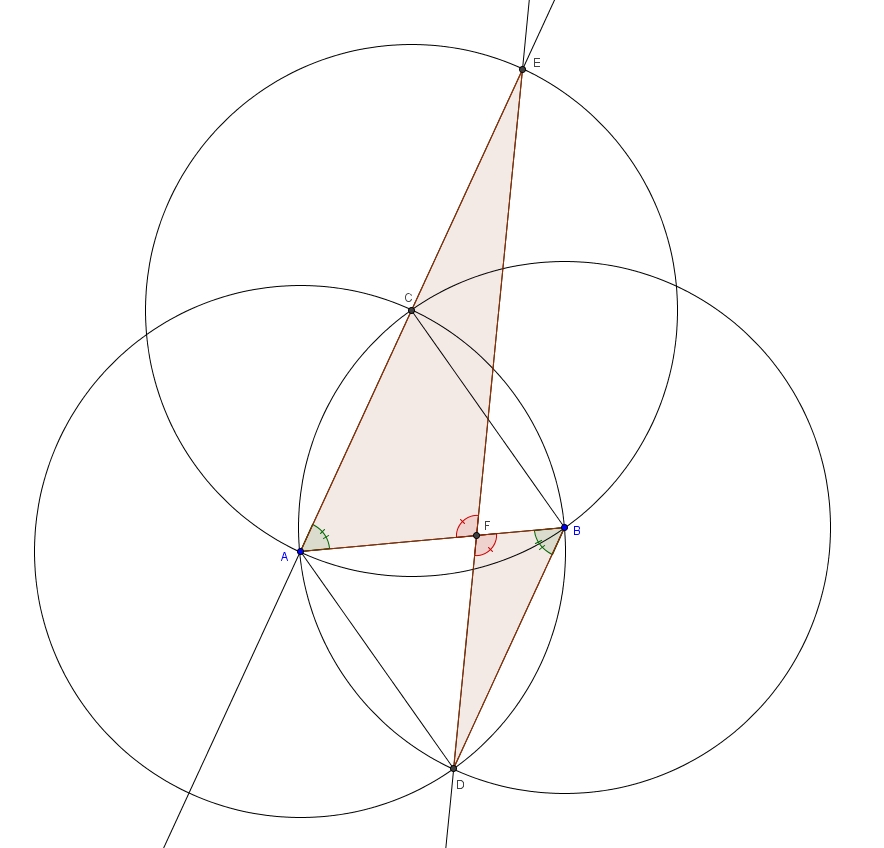
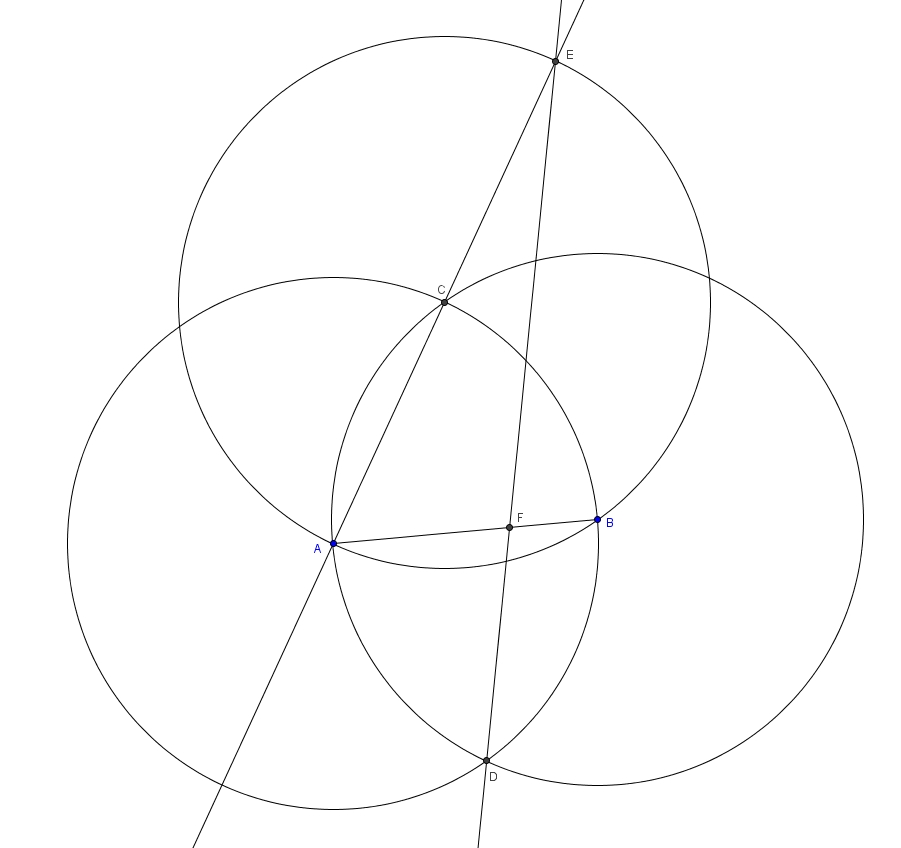 Notons d’abord que les trois cercles sont isométriques puisque la mesure de leur rayon est égale à la mesure du segment \(AB\). Considérons les triangles \(ABC\) et \(ABD\). Ce sont des triangles équilatéraux (chacun de leurs côtés est, justement, un rayon des trois cercles congrus). Les angles intérieurs d’un triangle équilatéral sont tous de \(60^{\circ}\). En particulier, les angles \(BAC\) et \(ABD\) valent tous les deux \(60^{\circ}\). \[m\angle BAC = m\angle ABD = 60^{\circ}\]
Notons d’abord que les trois cercles sont isométriques puisque la mesure de leur rayon est égale à la mesure du segment \(AB\). Considérons les triangles \(ABC\) et \(ABD\). Ce sont des triangles équilatéraux (chacun de leurs côtés est, justement, un rayon des trois cercles congrus). Les angles intérieurs d’un triangle équilatéral sont tous de \(60^{\circ}\). En particulier, les angles \(BAC\) et \(ABD\) valent tous les deux \(60^{\circ}\). \[m\angle BAC = m\angle ABD = 60^{\circ}\]