Élémentaire mon cher Archimède…

Le nombre π est un nombre irrationnel.

La preuve qui suit est une preuve qu’on dit « élémentaire » et elle possède d’ailleurs l’avantage principal de toutes les preuves élémentaires : elle nécessite peu de résultats préalables. Dans ce cas-ci, on fera appel à quelques résultats de base de calcul différentiel (par exemple, dériver un produit de fonctions [1] ou dériver un certain nombre de fois une fonction polynomiale [2]), au théorème fondamental du calcul différentiel et intégral et à quelques propriétés de la fonction sinus, à savoir en particulier que $$\sin (\pi )=0$$La preuve possède cependant les désavantages de (presque) toutes les preuves élémentaires de résultats difficiles : elle est plutôt longue, intriquée, et il est essentiellement impossible de justifier ou de donner une motivation pour les prochaines étapes, qui semblent parfois ne maintenir qu’un fil conducteur très ténu (non sans rappeler la preuve “élémentaire” de la valeur de ζ(2)). Dès lors, le lecteur perspicace se sent inévitablement trahi (désolé M. Pólya).

La preuve est essentiellement celle de Y. Iwamoto, parue dans le Journal of Osaka Institute of Science and Technology en 1949. La preuve de M. Iwamoto est une version plus forte de celle, plus célèbre, d’Ivan Niven [3] parue deux ans plus tôt. Dans sa monographie Irrational Numbers, Niven explique que sa preuve reprend et développe des idées basées sur celle de nul autre que Charles Hermite.

Comme cette preuve s’adresse à un public averti, on trouve dans la littérature peu de détails sur les étapes intermédiaires. Et comme mon blogue s’adresse à un public plus large, je vais tenter une approche plus près de celle empruntée par Michael Spivak dans son livre Calculus (4th edition), c’est-à-dire avec un peu plus d’explications. Ainsi, j’espère faire honneur malgré tout à M. Pólya [4] :

“The advanced reader who skips parts that appear too elementary may miss more than the less advanced reader who skips parts too complex.“

Dans ce qui suit, on notera $$f^{(k)}(x)$$la dérivée $k$^ième de la fonction $f$. On a donc en particulier pour les premières valeurs de $k$ : $$f^{(0)}(x)=f(x),f^{(1)}(x)=f^{\prime }(x),f^{(2)}(x)=f^{\prime \prime }(x)$$On considère d’abord la fonction suivante $$f_n(x)=\frac{x^n(1-x{)}^n}{n!}$$Il est évident que pour $$0<x<1$$la fonction satisfait $$0<f_n(x)<\frac{1}{n!}$$Si on développe le binôme entre parenthèses, et qu’on distribue par la suite $x^n$, on obtient au numérateur un polynôme de degré $2n$, c’est-à-dire qu’on peut exprimer la fonction $f_n$ comme 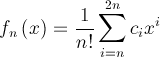$$f_n(x)=\frac{1}{n!}\sum _{i=n}^{2n}{c}_i{x}^i$$pour certaines valeurs entières de $c_i$ (on pourrait exprimer ces valeurs avec le binôme de Newton mais c’est, dans cette preuve, sans importance). On considère les dérivées $k$^ième de $f_n$. Il est clair que $$f_n^{(k)}(0)=0$$si $$k<n$$puisque dans ce cas, il ne reste que des termes en $x$, ou si $$k>2n$$puisque dans ce cas, on dérive un nombre plus grand de fois que le degré du polynôme. Pour $$n\le k\le 2n$$on a $$\begin{array}{rl}{f}_n^{(n)}(x)& =\frac{1}{n!}(n!c_n+\left(\text{des termes en }x\right))\\ \\ f_n^{(n+1)}(x)& =\frac{1}{n!}((n+1)!c_{n+1}+\left(\text{des termes en }x\right))\\ \\ & ⋮\\ \\ f_n^{(2n)}(x)& =\frac{1}{n!}(\left(2n\right)!c_{2n})\end{array}$$ce qui fait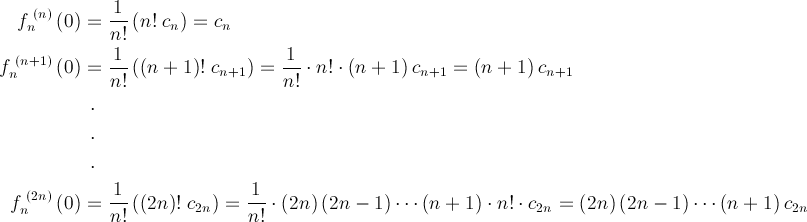 $$\begin{array}{rl}{f}_n^{(n)}(0)& =\frac{1}{n!}(n!c_n)=c_n\\ \\ f_n^{(n+1)}(0)& =\frac{1}{n!}((n+1)!c_{n+1})=\frac{1}{n!}\cdot n!\cdot (n+1)c_{n+1}=(n+1)c_{n+1}\\ \\ & ⋮\\ \\ f_n^{(2n)}(0)& =\frac{1}{n!}(\left(2n\right)!c_{2n})=\frac{1}{n!}\cdot \left(2n\right)(2n-1)\dots (n+1)\cdot n!\cdot c_{2n}=\left(2n\right)(2n-1)\dots (n+1)c_{2n}\end{array}$$Tous les termes à droites sont des nombres entiers. Ainsi, l’expression $$f_n^{(k)}(0)$$représente toujours un nombre entier, quelle que soit la valeur de $k$. 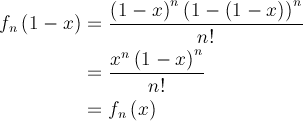Par ailleurs, on a $$\begin{array}{rl}{f}_n(1-x)& =\frac{{(1-x)}^n{(1-(1-x))}^n}{n!}\\ \\ & =\frac{x^n{(1-x)}^n}{n!}\\ \\ & =f_n(x)\end{array}$$ce qui nous permet de trouver en particulier $$f_n^{(k)}(x)={(-1)}^k{f}_n^{(k)}(1-x)$$et de conclure que l’expression$$f_n^{(k)}(1)$$représente elle aussi toujours un nombre entier. Avant d’introduire d’autres fonctions savamment construites à partir de $f_n$, on s’attarde à une courte remarque. Si $a$ est un nombre positif, alors pour tout $ϵ>0$, on a, pour un $n$ suffisamment grand, $$\frac{a^n}{n!}<ϵ$$On peut d’abord observer que si $n\ge 2a$, on a $$\begin{array}{rl}\frac{a^{n+1}}{(n+1)!}& =\frac{a\cdot a^n}{(n+1)n!}\\ \\ & =\frac{a}{n+1}\cdot \frac{a^n}{n!}\\ \\ & <\frac{1}{2}\cdot \frac{a^n}{n!}\end{array}$$
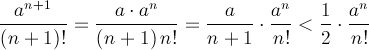
Incidemment, en posant $n_0$ un nombre naturel tel que$$n_0\ge 2a$$qu’importe la valeur de $$\frac{a^{n_0}}{\left(n_0\right)!}$$les valeurs successives seront 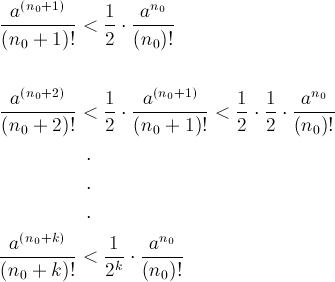$$\begin{array}{rl}\frac{a^{(n_0+1)}}{(n_0+1)!}& <\frac{1}{2}\cdot \frac{a^{n_0}}{\left(n_0\right)!}\\ \\ \frac{a^{(n_0+2)}}{(n_0+2)!}& <\frac{1}{2}\cdot \frac{a^{(n_0+1)}}{(n_0+1)!}<\frac{1}{2}\cdot \frac{1}{2}\cdot \frac{a^{n_0}}{\left(n_0\right)!}\\ \\ & ⋮\\ \\ \frac{a^{(n_0+k)}}{(n_0+k)!}& <\frac{1}{2^k}\cdot \frac{a^0}{\left(n_0\right)!}\end{array}$$De cela on tire, en choisissant correctement une valeur de $k$ assez grande, $$\frac{a^{n_0}}{\left(n_0\right)!ϵ}<2^k$$et donc obtenir$$\frac{a^{(n_0+k)}}{(n_0+k)!}<ϵ$$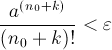soit le résultat attendu. On s’attaque maintenant à l’irrationalité du nombre $\pi$. On va cependant démontrer un résultat encore plus fort, l’irrationalité de ${\pi }^2$. En effet, si $\pi$ était rationnel, alors ${\pi }^2$ serait certainement lui aussi rationnel. La preuve fonctionne par contradiction. On suppose donc que ${\pi }^2$ est rationnel et que$${\pi }^2=\frac{a}{b}$$avec $a$ et $b$ des entiers positifs premiers entre eux. On introduit la fonction $G$ suivante $$G(x)=b^n({\pi }^{2n}{f}_n(x)-{\pi }^{2n-2}{f}_n^{\prime \prime }(x)+{\pi }^{2n-4}{f}_n^{\left(4\right)}(x)-\dots +{(-1)}^n{f}_n^{\left(2n\right)}(x))$$Lorsqu’on distribue $b^n$ dans la parenthèse, on obtient des coefficients des termes en $f_n^{\left(k\right)}$ de la forme $$\begin{array}{rl}{b}^n{\pi }^{2n-2k}& =b^n{\pi }^{2(n-k)}\\ \\ & =b^n{\left({\pi }^2\right)}^{n-k}\\ \\ & =b^n{\left(\frac{a}{b}\right)}^{n-k}\\ \\ & =a^{n-k}{b}^k\end{array}$$c’est-à-dire tous des nombres entiers. Et puisque $$f_n^{\left(k\right)}(0)$$et $$f_n^{\left(k\right)}(1)$$sont des entiers, alors$$G(0)$$et$$G(1)$$sont eux aussi des entiers. On dérive la fonction $G$ deux fois $$G^{\prime \prime }(x)=b^n({\pi }^{2n}{f}_n^{\prime \prime }(x)-{\pi }^{2n-2}{f}_n^{\left(4\right)}(x)+{\pi }^{2n-4}{f}_n^{\left(6\right)}(x)-\dots +{(-1)}^n{f}_n^{(2n+2)}(x))$$Le dernier terme, $${(-1)}^n{f}_n^{(2n+2)}(x)$$est bien sûr zéro. Maintenant, on remarque qu’en multipliant $G$ par ${\pi }^2$, on obtient $$\begin{array}{rl}{\pi }^{2}G(x)& ={\pi }^2\left(b^n({\pi }^{2n}{f}_n(x)-{\pi }^{2n-2}{f}_n^{\prime \prime }(x)+{\pi }^{2n-4}{f}_n^{\left(4\right)}(x)-\dots +{(-1)}^n{f}_n^{\left(2n\right)}(x))\right)\\ \\ & =b^n({\pi }^{2n+2}{f}_n(x)-{\pi }^{2n}{f}_n^{\prime \prime }(x)+{\pi }^{2n-2}{f}_n^{\left(4\right)}(x)-{\pi }^{2n-4}{f}_n^{\left(6\right)}(x)+\dots +{(-1)}^n{\pi }^2{f}_n^{\left(2n\right)}(x))\end{array}$$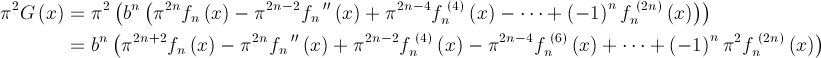et qu’il est possible de faire la somme de $G^{\prime \prime }(x)$ et ${\pi }^{2}G(x)$ et d’observer que tous les termes s’annulent sauf un, afin d’obtenir $$\begin{array}{rl}{G}^{\prime \prime }(x)+{\pi }^{2}G(x)& =b^n{\pi }^{2n+2}{f}_n(x)\\ \\ & =b^n{\left(\frac{a}{b}\right)}^n{\pi }^2{f}_n(x)\\ \\ & ={\pi }^2{a}^n{f}_n(x)\end{array}$$On introduit enfin une dernière fonction $H$ $$H(x)=G^{\prime }(x)\sin \left(\pi x\right)-\pi G(x)\cos \left(\pi x\right)$$Lorsqu’on dérive cette fonction, on obtient $$H^{\prime }(x)=G^{\prime \prime }(x)\sin \left(\pi x\right)+\pi G^{\prime }(x)\cos \left(\pi x\right)-\pi G^{\prime }(x)\cos \left(\pi x\right)+{\pi }^{2}G(x)\sin \left(\pi x\right)$$ce qui se simplifie en regroupant les deux termes qui s’annulent et en effectuant la mise en évidence $$\begin{array}{rl}{H}^{\prime }(x)& =G^{\prime \prime }(x)\sin \left(\pi x\right)+{\pi }^{2}G(x)\sin \left(\pi x\right)\\ \\ & =(G^{\prime \prime }(x)+{\pi }^{2}G(x))\sin \left(\pi x\right)\end{array}$$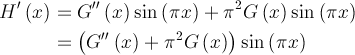En remplaçant l’expression entre parenthèses, on obtient 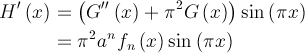$$\begin{array}{rl}{H}^{\prime }(x)& =(G^{\prime \prime }(x)+{\pi }^{2}G(x))\sin \left(\pi x\right)\\ \\ & ={\pi }^2{a}^n{f}_n(x)\sin \left(\pi x\right)\end{array}$$On considère maintenant l’intégrale définie suivante 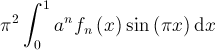$${\pi }^2{\int }_0^1{a}^n{f}_n(x)\sin \left(\pi x\right)\text{d}x$$Le théorème fondamental du calcul différentiel et intégral nous permet d’écrire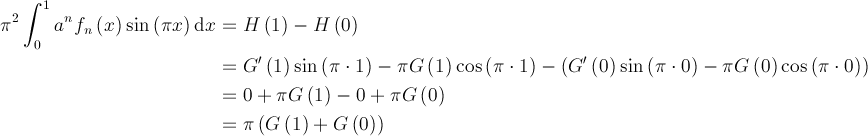 $$\begin{array}{rl}{\pi }^2{\int }_0^1{a}^n{f}_n(x)\sin \left(\pi x\right)\text{d}x& =H(1)-H(0)\\ \\ & =G^{\prime }(1)\sin (\pi \cdot 1)-\pi G(1)\cos (\pi \cdot 1)-(G^{\prime }(0)\sin (\pi \cdot 0)-\pi G(0)\cos (\pi \cdot 0))\\ \\ & =0+\pi G(1)-0+\pi G(0)\\ \\ & =\pi (G(1)+G(0))\end{array}$$On a, à droite, une somme de termes constants multipliée par $\pi$. De cela, en divisant par $\pi$, on tire l’intégrale définie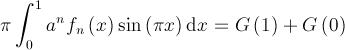 $$\pi {\int }_0^1{a}^n{f}_n(x)\sin \left(\pi x\right)\text{d}x=G(1)+G(0)$$c’est-à-dire un nombre entier ! 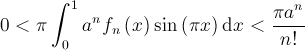Or, comme on avait remarqué, on a $$0<f_n(x)<\frac{1}{n!}$$pour$$0<x<1$$Conséquemment, en multipliant par $\pi a^n$, un nombre positif, on a$$0<\pi a^n{f}_n(x)\sin \left(\pi x\right)<\frac{\pi a^n}{n!}$$et donc aussi, en inspectant les bornes de l’intégrale,$$0<\pi {\int }_0^1{a}^n{f}_n(x)\sin \left(\pi x\right)\text{d}x<\frac{\pi a^n}{n!}$$Mais comme ce raisonnement est indépendant de la valeur de $n$, on n’a qu’à choisir un $n$  assez grand afin d’obtenir 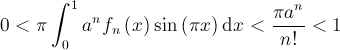$$0<\pi {\int }_0^1{a}^n{f}_n(x)\sin \left(\pi x\right)\text{d}x<\frac{\pi a^n}{n!}<1$$ce qui est la contradiction recherchée ! L’intégrale est un nombre entier, mais il n’y a évidemment aucun nombre entier strictement supérieur à $0$ et strictement inférieur à $1$. Notre prémisse de départ s’avère donc fausse : ${\pi }^2$ est irrationnel.

[1]  $${(f\cdot g)}^{\prime }=f^{\prime }g+f{g}^{\prime }$$[2] Si $$f(x)=x^a$$on a $$f^{\left(k\right)}(x)=a(a-1)(a-2)\dots (a-k+1)a^{a-k}$$et comme à chaque fois qu’on dérive le degré diminue de $1$, si on dérive $a$ fois une fonction polynomiale de degré $a$, on obtient une constante et si on dérive la fonction polynomiale plus de $a$ fois, on obtient des termes nuls.

[3] Voici la preuve originale d’Ivan Niven parue dans le Bulletin of American Mathematical Society 53 (1947), 509.

[4] George Pólya (1954) dans Induction and Analogy in Mathematics

Références supplémentaires : Michael Spivak (2008), Calculus (4th edition)

Martin Aigner et Günter M. Ziegler (2010), Proofs from THE BOOK (4th edition)

Ivan Niven (1965), Irrational Numbers