La cible

La version classée “Visa Général”

Un problème classique de probabilité géométrique (qui s’intègre par exemple au programme de troisième secondaire) est le suivant :

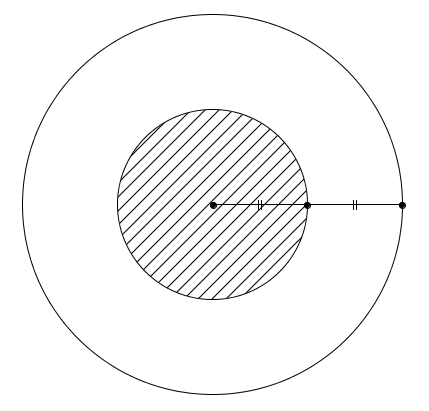
On sélectionne un point au hasard sur une cible circulaire. Quelle est la probabilité que le point choisi soit plus prêt du centre que de la circonférence de la cible ?

Il semble assez évident pour les élèves de délimiter correctement de manière intuitive les zones par deux disques concentriques.

Plusieurs élèves évaluent néanmoins incorrectement (souvent sans avoir fait un seul calcul ou réfléchi au rapport des aires de figures semblables) la probabilité de choisir un point dans la zone hachurée à \(\frac{1}{2}\) (parce que le rayon du disque hachuré correspond à la moitié du rayon du grand disque). Or, si le petit disque possède un rayon de \(r\) et le grand \(2r\), on a la probabilité \(P\) recherchée \begin{align*}P&= \frac{\text{Aire du petit disque hachuré}}{\text{Aire du grand disque}} \\ \\ &= \frac{\pi r^{2}}{\pi \left(2r\right)^{2}} \\ \\ &=\frac{\pi r^{2}}{4\pi r^{2}} \\ \\ &= \frac{1}{4}\end{align*}ce qui n’est pas la solution attendue par ces élèves ! Il y a donc un certain élément de surprise.

La version “Pour Adultes”

Quel ne fut pas mon plaisir de tomber sur un problème similaire mais cette fois-ci pour les plus grands. On n’a essentiellement qu’à changer un seul mot.

On sélectionne un point au hasard sur une cible carrée. Quelle est la probabilité que le point sélectionné soit plus prêt du centre du carré que d’un de ses côtés ?

Je vous conseille bien fortement d’essayer de trouver la solution par vous-même avant de continuer la lecture. Quel plaisir ! Ce problème faisait partie de la compétition Putnam 1989. Dans l’énoncé original, on demande que la réponse finale soit sous la forme \[\frac{a+b\sqrt{c}}{d}\]avec \(a\), \(b\), \(c\) et \(d\) entiers. C’est ce que nous allons faire.

Un analyse sommaire peut nous conduire à identifier des points « évidents » situés les frontières (en rouge, ci-bas).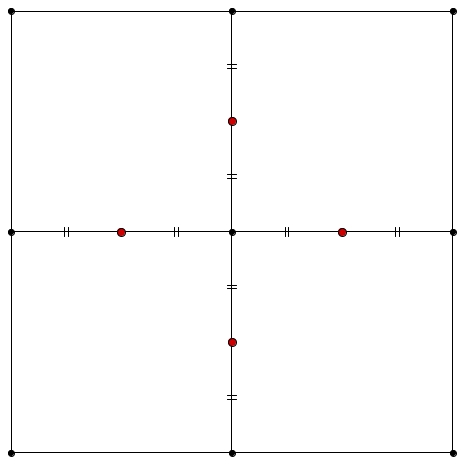

Or, nos « réflexes » habituels semblent de prime abord futiles. La région à considérer n’est certainement pas un carré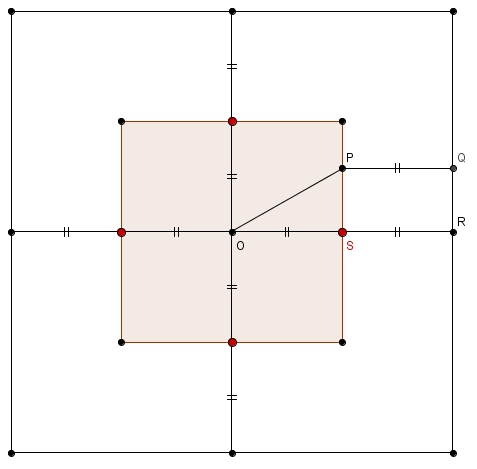
car, ici, comme \[m\overline{OS} = m\overline{SR} = m\overline{PQ}\]et \(\overline{OP}\) est l’hypoténuse d’un triangle rectangle dont \(\overline{OS}\) est une cathète, on a clairement que \[m\overline{OP}>m\overline{PQ}\]Le point \(P\) est donc plus prêt du côté du carré que du centre. La région à considérer n’est pas non plus un disque

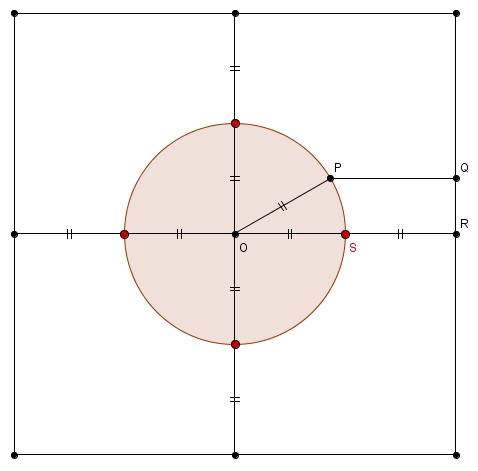puisque si \[m\overline{OS} = m\overline{SR}\]on ne peut clairement pas avoir en même temps également \[m\overline{OS} = m\overline{OP} = m\overline{PQ}\]si \(P\) n’est pas en \(S\). Le point \(P\) est donc plus prêt du centre que du côté du carré.

 

L’ensemble de points équidistants d’un point et d’une droite est une parabole. La région à considérer est donc délimitée par quatre paraboles qui ont pour foyer le centre du carré et comme droites directrices les droites qui supportent les côtés du carré.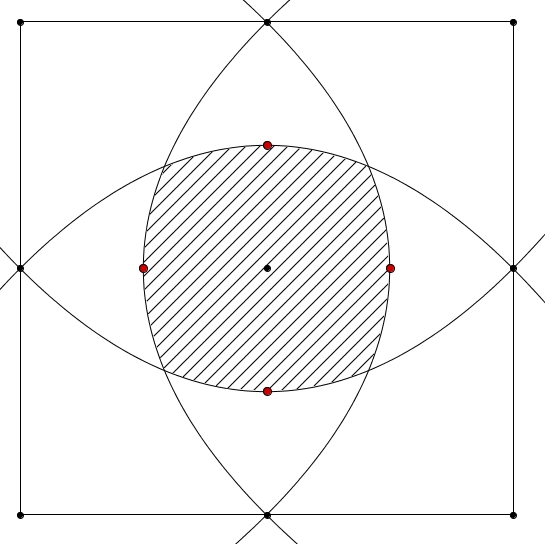On s’affaire donc à trouver l’aire de cette région hachurée. La tâche s’avère de prime abord ardue. Cependant, il est possible d’utiliser les symétries de la figure à notre avantage. On place d’abord le tout dans un repère cartésien. Les sommets du carré sont \((1,\, 1)\), \((-1,\, 1)\), \((-1,\, -1)\) et \((1,\, -1)\).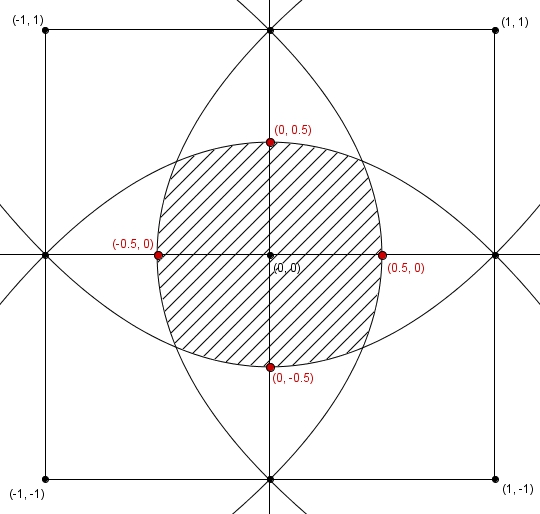

En vertu des symétries de la figure, il nous est possible de nous concentrer seulement sur la partie située dans le premier quadrant.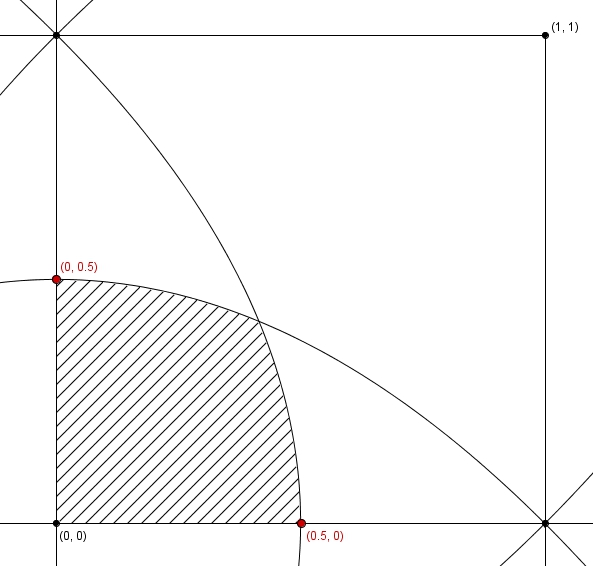

Qui plus est, il est possible de ne s’attarder qu’à la moitié de cette dernière région.

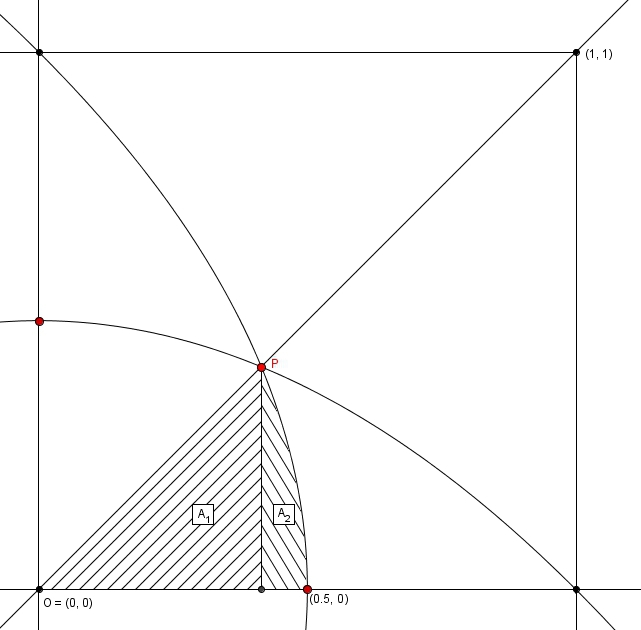Ce « croissant de parabole » correspond à la moitié de la région à considérer dans le premier quadrant. On note au passage que l’aire du carré dans ce premier quadrant est 1 (pratique pour calculer des probabilités). Le « croissant » est à son tour divisé en deux parties : la zone de forme triangulaire \(A_{1}\) et la zone \(A_{2}\). On cherche l’aire de ces zones. Pour y arriver, on aura besoin des coordonnées de \(P\).

L’équation de la parabole qui nous intéresse est \[\left(y-k\right)^{2}=4c\left(x-h\right)\]où \(h\) et \(k\) sont les coordonnées du sommet de la parabole et \(c\) est la distance focale (orientée). On a donc \begin{align*}y^{2}&=4\left(-\frac{1}{2}\right)\left(x-\frac{1}{2}\right) \\ \\ &=-2\left(x-\frac{1}{2}\right) \\ \\ &=1-2x \end{align*}On isole ensuite \(y\) dans \[y^{2}=1-2x\]en prenant la racine carrée \[y = \pm\sqrt{1-2x}\]On ne s’intéressera qu’à la branche située au dessus de l’axe des abscisses. Ainsi, on ne garde que la racine positive \[y = \sqrt{1-2x}\]On cherche ensuite les coordonnées de \(P\), le point d’intersection entre la courbe d’équation \[y = \sqrt{1-2x}\]et la droite d’équation \[y=x\]Par comparaison, on a \[x = \sqrt{1-2x}\]puis en élevant au carré \[x^{2}=1-2x\]On obtient un trinôme du deuxième degré \[x^{2}+2x-1=0\]qu’on peut résoudre en compétant le carré \begin{align*}x^{2}+2x-1&=0 \\ \\ x^{2}+2x+1 &= 2 \\ \\ \left(x+1\right)^{2}&=2 \\ \\ x+1 &= \pm\sqrt{2} \\ \\ x&=-1\pm\sqrt{2}\end{align*}Comme \(P\) est dans le premier quadrant, on ne garde que la solution positive \[x=-1+\sqrt{2}\]et puisque \[y = x\]les coordonnées de \(P\) sont \[\left(-1+\sqrt{2},\,-1+\sqrt{2}\right)\]Il nous est donc déjà possible de trouver l’aire du triangle, que l’on a identifié comme \(A_{1}\). \begin{align*}A_{1}&= \frac{\left(-1+\sqrt{2}\right)\left(-1+\sqrt{2}\right)}{2} \\ \\ &=\frac{1-2\sqrt {2}+2}{2} \\ \\ &=\frac{3-2\sqrt{2}}{2}\end{align*}Il reste à trouver l’aire de la région sous la courbe, celle identifiée comme \(A_{2}\). On pose l’intégrale définie suivante \[A_{2}=\int_{-1+\sqrt{2}}^{\frac{1}{2}}\sqrt{1-2x}\,\text{d}x\]On effectue le changement de variables suivant \begin{align*}u&=1-2x \\ \\ \text{d}u&=-2\text{d}x \\ \\ -\frac{1}{2}\text{d}u &= \text{d}x\end{align*}
en n’oubliant pas les bornes de l’intégrale \[1-2\left(\frac{1}{2}\right) = 1-1=0\]et \[1-2\left(-1+\sqrt{2}\right)=1+2-2\sqrt{2}=3-2\sqrt{2}\]On a donc \begin{align*}\int_{3-2\sqrt{2}}^{0} \sqrt{u} \cdot \left(-\frac{1}{2}\right) \text{d}u &= -\frac{1}{2}\int_{3-2\sqrt{2}}^{0}\sqrt{u}\,\text{d}u \\ \\ &=-\frac{1}{2}\int_{3-2\sqrt{2}}^{0}u^{\frac{1}{2}}\,\text{d}u \\ \\ &=-\frac{1}{2}\cdot \left[\frac{2}{3}u^{\frac{2}{3}}\right]_{3-2\sqrt{2}}^{0} \\ \\ &=-\frac{1}{2}\left(0-\frac{2}{3}\left(3-2\sqrt{2}\right)^{\frac{3}{2}}\right) \\ \\ &= \frac{1}{2}\left(3-2\sqrt{2}\right)^{\frac{3}{2}}\end{align*}Ainsi, on obtient l’aire \(A_{2}\) \begin{align*}A_{2}&= \frac{1}{3}\left(3-2\sqrt{2}\right)^{\frac{3}{2}} \\ \\  &=\frac{1}{3}\left(\!\sqrt{3-2\sqrt{2}}\,\right)^{\! 3}\end{align*}L’expression entre parenthèses se simplifie.  Le nombre sous la racine est effectivement un carré.  On pourrait poser \begin{align*}\sqrt{3-2\sqrt{2}}&=a+b\sqrt{2} \\ \\ \\ 3-2\sqrt{2}&=\left(a+b\sqrt{2}\right)^{2} \\ \\ &=a^{2}+2ab\sqrt{2} + 2b^{2} \\ \\ &=a^{2} + 2b^{2}+2ab\sqrt{2} \end{align*}En égalant les parties entières du nombre et les coefficients de \(\sqrt{2}\), on obtient les équations suivantes \[3 = a^{2}+2b^{2}\]et \[-2=2ab\]Par chance, la dernière devient, en divisant par \(2\), \[-1=ab\]Il faut donc que \(a\) et \(b\) prennent les valeurs de \(1\) et \(-1\). Dans quel ordre ? Il suffit de remarquer qu’on veut un nombre \[a+b\sqrt{2}\]positif. On pose donc \[a = -1, \, b = 1\]ce qui satisfait bien entendu la deuxième équation mais aussi la première, afin d’obtenir \[A_{2} = \frac{\left(-1+\sqrt{2}\right)^{3}}{3}\]L’aire totale est donc de \[A_{1}+A_{2} = \frac{3-2\sqrt{2}}{2} + \frac{\left(-1+\sqrt{2}\right)^{3}}{3}\]En développant on a \[A_{1}+A_{2} = \frac{3-2\sqrt{2}}{2}+\frac{5\sqrt{2}-7}{3}\]puis en mettant sur dénominateur commun \[A_{1}+A_{2} = \frac{9-6\sqrt{2}}{6}+\frac{10\sqrt{2}-14}{6}\]on obtient finalement \[A_{1}+A_{2}=\frac{-5+4\sqrt{2}}{6}\]Comme le carré du premier quadrant à une aire de \(1\), il ne reste qu’à doubler ce résultat afin d’obtenir la probabilité recherchée \[2\left(A_{1}+A_{2}\right) = \frac{-5+4\sqrt{2}}{3}\]ce qui correspond à un peu moins de \(22\%\).