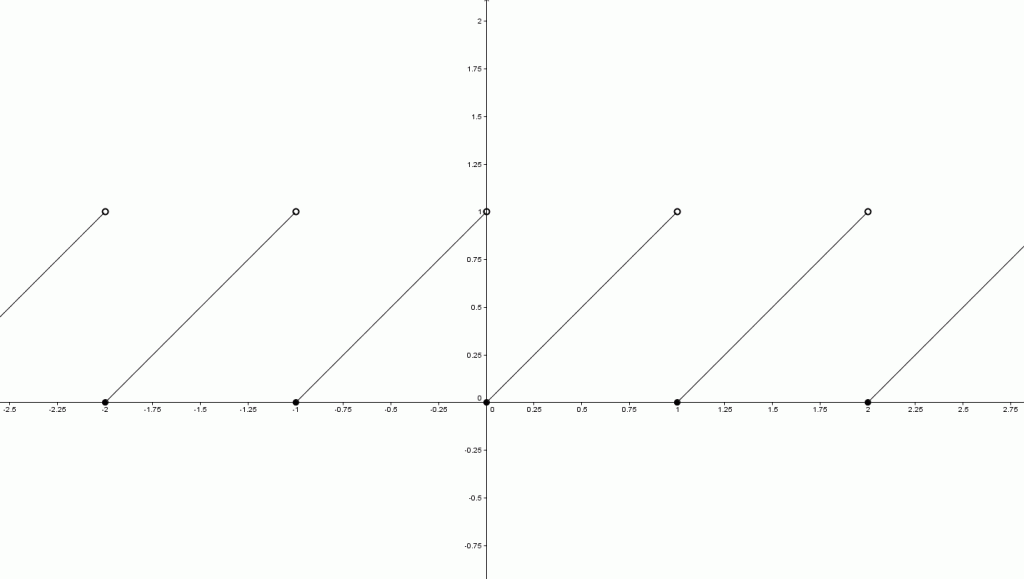En quatrième secondaire, les élèves sont introduits aux fonctions périodiques de manière très large et générale. Ils apprennent entre autres ce qu’est une période, comment l’identifier et quoi faire avec. Ils reconnaissent des représentations graphiques de diverses de fonctions périodiques (mais sans étudier les règles) et, à partir du graphique, sont capables d’identifier certaines propriétés de ces fonctions. Les plus avantureux comprennent que si f est une fonction périodique de période p, alors
![]()
Mais tout cela est fait sans étudier une seule fonction périodique particulière (dont on connaîtrait la règle, par exemple), les fonctions trigonométriques étant au programme de cinquième secondaire. Les élèves de quatrième secondaire ayant cependant étudié la fonction partie entière (ou fonction plus grand entier inférieur ou égal à…, notée [x]), je leur ai demandé de tracer la fonction suivante :
![]()
fonction très intéressante à tracer (allez-y !) et dont voici le graphique
Quelques élèves y sont parvenus. J’ai tracé ce graphique en classe lors de la correction du devoir. Et puis spontanément j’ai fait avec eux l’étude de cette fonction périodique, bien que cela n’était pas prévu dans la leçon. Et là sans préavis survient la question qui tue : cette fonction possède-t-elle un maximum ? Génial ! Quelle occasion en or de leur montrer ceci.