On avait déjà vu ici cette image :
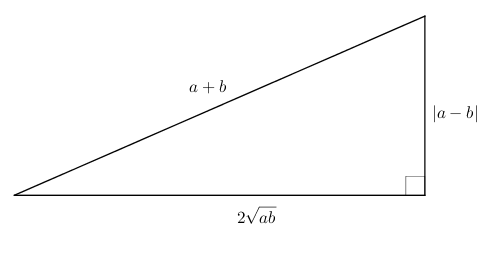
Le triangle est rectangle car la relation de Pythagore est vérifiée : \begin{align*}\left(2\sqrt{ab}\right)^{2} + \left(\left|a-b\right|\right)^{2} &= \left(2\sqrt{ab}\right)^{2}+\left(a-b\right)^{2} \\ \\ &= 4ab + a^{2}-2ab+b^{2} \\ \\ &= a^{2}+2ab+b^{2} \\ \\ &= \left(a+b\right)^{2}\end{align*}
Les mesures des cathètes étant strictement inférieures à celle de l’hypoténuse, on trouve \[a+b > 2\sqrt{ab}\]ou, en divisant par \(2\), \[\frac{a+b}{2}>\sqrt{ab}\]On peut vérifier qu’on a l’égalité \[\frac{a+b}{2} = \sqrt{ab}\]si \(a = b\).
Voici une autre « preuve sans mots ».
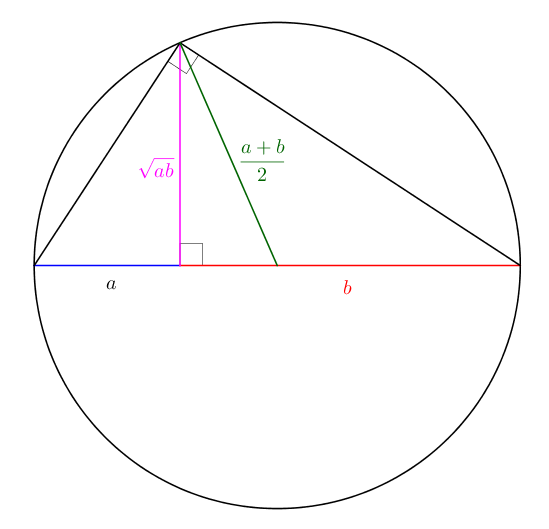
Le cercle de diamètre \(\textcolor{Blue}{a} + \textcolor{Red}{b}\) a un rayon \(\textcolor{Green}{\frac{a+b}{2}}\). Le grand triangle inscrit est sous-tendu par un diamètre, il est donc rectangle. La hauteur \(\textcolor{Magenta}{h}\) relative à l’hypoténuse est \[\frac{\textcolor{Magenta}{h}}{\textcolor{Blue}{a}}= \frac{\textcolor{Red}{b}}{\textcolor{Magenta}{h}}\]ce qui fait \[\textcolor{Magenta}{h}^{2} = \textcolor{Blue}{a}\textcolor{Red}{b}\]ou \[\textcolor{Magenta}{h} = \textcolor{Magenta}{\sqrt{\textcolor{Blue}{a}\textcolor{Red}{b}}}\]
La mesure de l’hypoténuse d’un triangle rectangle étant strictement supérieure à celles de ses cathètes, on a bien \[\textcolor{Green}{\frac{a+b}{2}}>\textcolor{Magenta}{\sqrt{ab}}\]Encore, une fois, on peut vérifier qu’on a l’égalité \[\textcolor{Green}{\frac{a+b}{2}}=\textcolor{Magenta}{\sqrt{ab}}\]si \(a = b\).