Le théorème de Frégier (ou un peu de géométrie analytique)

En feuilletant The Penguin Dictionary of Curious and Interesting Geometry, je suis tombé sur le théorème de Frégier (sans démonstration).  Quel résultat surprenant !  Fasciné, j’ai voulu en savoir davantage puisque j’en n’avais jamais eu connaissance.  Je me suis donc dirigé avec enthousiasme sur MathWorld, afin d’y trouver plus de détails.  Malheureusement, aucune démonstration là non-plus.  Et l’unique référence de MathWorld concernant le théorème de Frégier est… The Penguin Dictionary of Curious and Interesting Geometry.  Hummmm…

Le théorème de Frégier

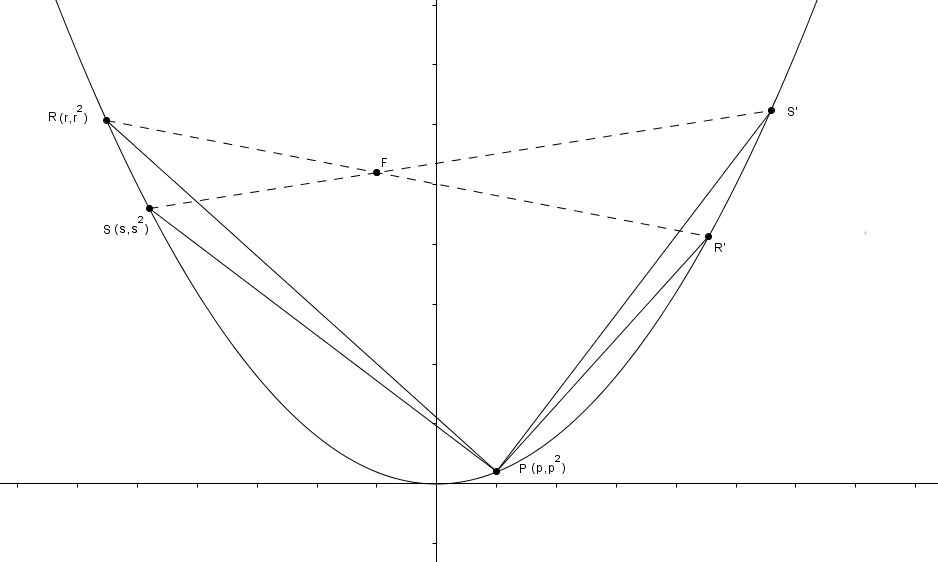
Dans une parabole ou une ellipse, d’un point P, on trace des segments perpendiculaires (angles droits qui ont leur sommet en P).  Les côtés des angles droits coupent la parabole ou l’ellipse.  Les segments qui joignent les points d’intersection des angles et de la conique passent tous par F, le point de Frégier.

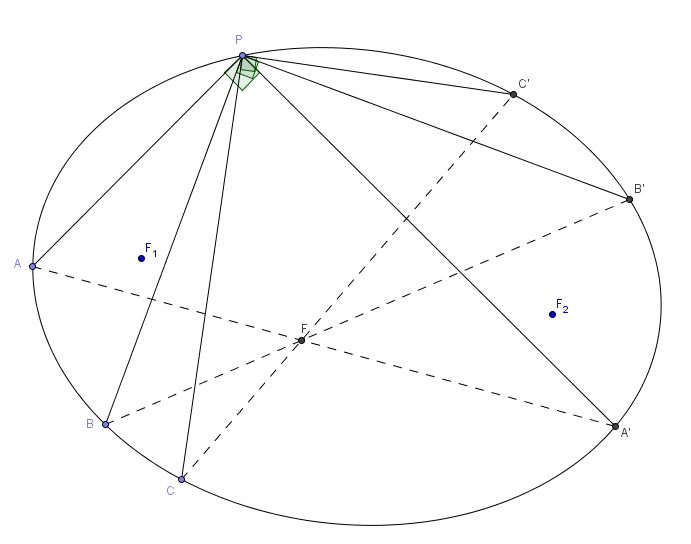Vous pouvez télécharger l’applet Géogébra ici : https://www.thedudeminds.net/blog/2010100601/

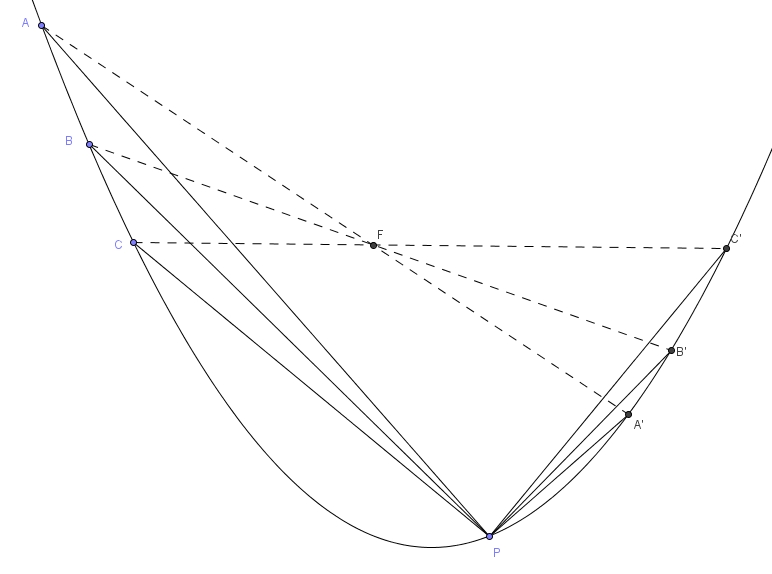
Vous pouvez télécharger l’applet Géogébra ici : https://www.thedudeminds.net/blog/2010100602/

Je n’ai rien trouvé ailleurs sur la toile sur ce théorème, alors j’ai décidé d’entreprendre une petite démonstration dans le cas de la parabole.  La géométrie analytique ne fait pas dans l’élégance, mais elle a l’avantage de bien fonctionner, sans surprise.  Considérons l’image suivante :

On trouve d’abord l’équation de PR.  Sa pente est

Le numérateur se factorise (c’est une différence de carrés)

et se simplifie.  Il reste donc simplement

La pente de la droite perpendiculaire à PR, soit PR’, est l’opposée de l’inverse de la pente de PR, c’est-à-dire

L’équation de PR’ est donc de la formeOn peut trouver la valeur de ben remplaçant x et y par les coordonnées de P, soit (p, p²).  On obtientsoitL’équation de PR’ est donc

On trouve les coordonnées de R’ en résolvant le système d’équations.  On sait que l’équation de la parabole est

ce qui fait

En envoyant tous les termes à gauche, on obtient un trinôme du deuxième degré (en x) égal à zéro.

La formule quadratique nous donnera les solutions (pratique !)  Une de ces solutions sera certainement

puisque la droite PR’ croise la parabole en P (en particulier).  L’autre solution sera l’abscisse de R’.  Le calcul du discriminant

donne

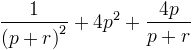En mettant sur dénominateur commun, on obtient

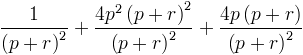et donc

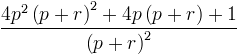Le numérateur est un trinôme carré parfait de la forme

qui se factorise en posant

et

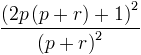On obtient doncque l’on peut aussi écrire en distribuant 2p dans la parenthèse

La formule quadratique nous donne donc

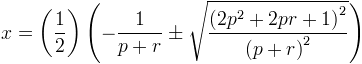En extrayant la racine carrée, on obtient

ce qui fait

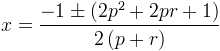Si on considère la première solution, on a

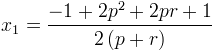ce qui fait

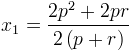Et après mise en évidence

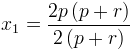et simplification des facteurs, 0n obtient le résultat attendu, à savoir l’abscisse de P.

C’est l’autre solution qui nous intéresse, l’abscisse de R’

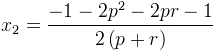qui fait

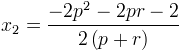Après mise en évidence de -2

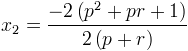et simplification, on obtient

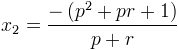Voilà ! Les coordonnées de R’ sont donc

Il n’est pas surprenant que les coordonnées de R’ dépendes de celles de P et de R.  Trouvons l’équation de RR’.  La pente de RR’ est

Le numérateur étant une différence de carrés, on le factorise

et on simplifie

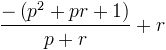On met ensuite sur dénominateur commun

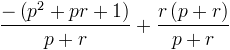ce qui donne

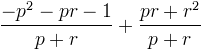puis

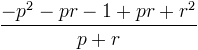En simplifiant les termes semblables, on obtientL’équation de RR’ est donc de la forme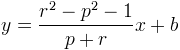Encore une fois on trouve b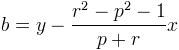en remplaçant x et y par les coordonnées de R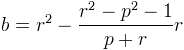ce qui fait en mettant sur dénominateur communet en distribuant

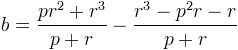et finalement en simplifiant un peu

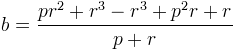on obtient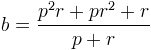L’équation de RR’ est donc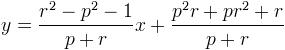

Par ailleurs, le même raisonnement utilisant les points S et S’ (au lieu de R et R’) nous permettrait de trouver l’équation de SS’

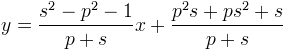Pour trouver les coordonnées de F, il suffit de résoudre le système d’équations

En regroupant les termes en x à gauche et les autres à droite, on obtient

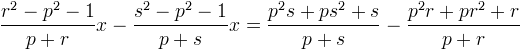ce qui fait

En mettant sur dénominateur commun, on obtient

ce qui nous permet d’écrire

En distribuant, on obtient d’abord

puis

Quelques termes se simplifient à gauche et à droite.  La mise en évidence de –p à droite donne

ce qui, de façon assez surprenante, donne tout simplement

soit l’abscisse de F.  Cette abscisse ne dépend ni de R, ni de S, que de P.  Quelle est l’ordonnée de F ? Il suffit de remplacer x par –p dans l’une ou l’autre des équations (RR’ ou SS’).  On obtient

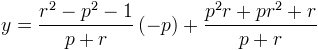ce qui faitpuis en simplifiant un peu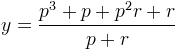Il nous est possible d’effectuer une mise en évidence double au numérateur.  On obtient

puisEt non sans une certaine satisfaction, on peut simplifierLes coordonnées de F sont donc

Or, comme

Le lieu de point de F lorsqu’on déplace P sur la parabole sera une parabole isométrique à la parabole originale mais déplacée de une unité vers le haut.  Dans un cas un peu plus général que vous pourrez vérifier chers lecteurs, si l’équation de la parabole est

le lieu de point F sera