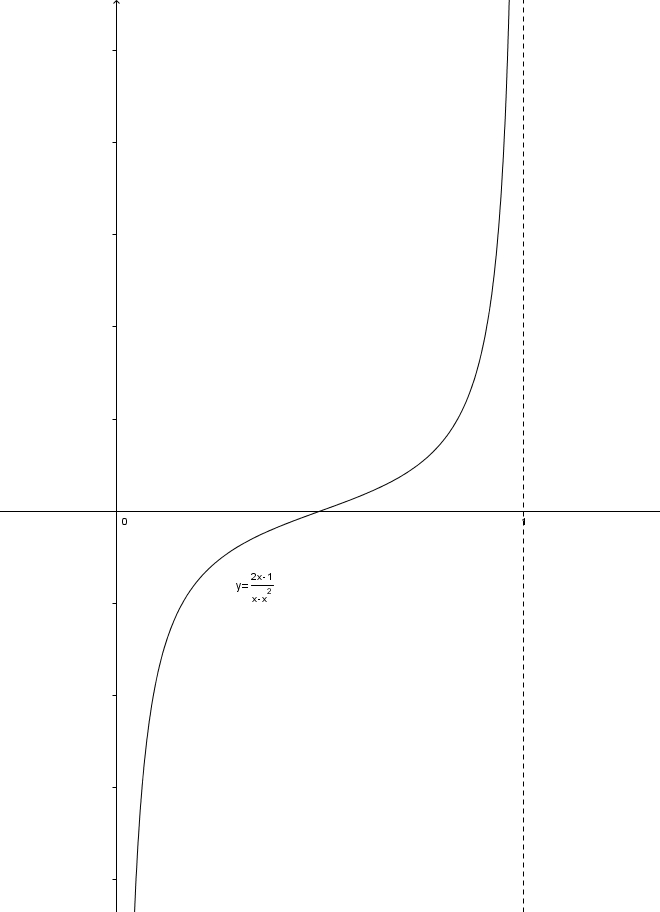
La relation
associe à chaque réel x dans l’intervalle
un unique réel y dans l’intervalle
et, inversement, associe à chaque réel y dans l’intervalle
un unique réel x dans l’intervalle
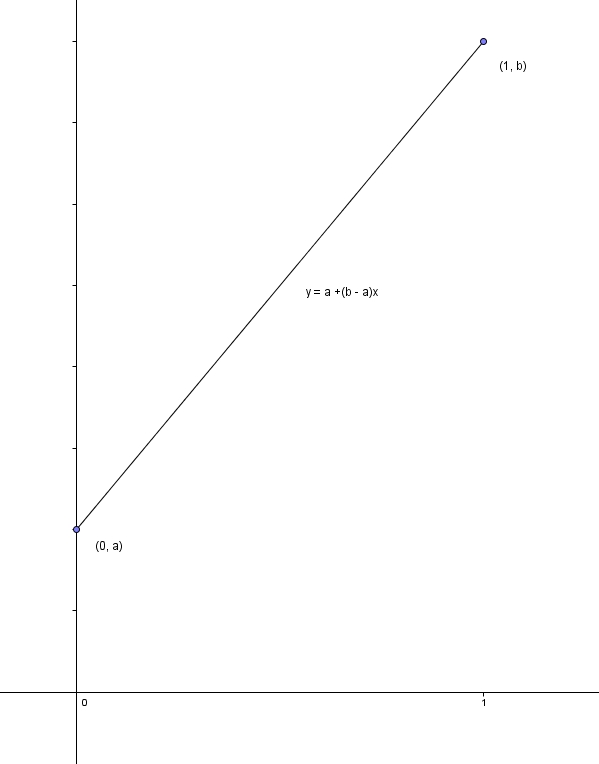
Quant à elle, la relation
associe à chaque réel x dans l’intervalle
un unique réel y et, inversement, associe à chaque réel y un unique réel x dans l’intervalle
