Une jolie image…

Une jolie image chez Futility Closet, reproduite ici – merci, Géogébra – m’inspire ce billet. C’est beau et c’est un opportun prétexte pour trouver quelques valeurs exactes supplémentaires et dépoussiérer (dans mon cas) le livre XIII des Éléments d’Euclide.

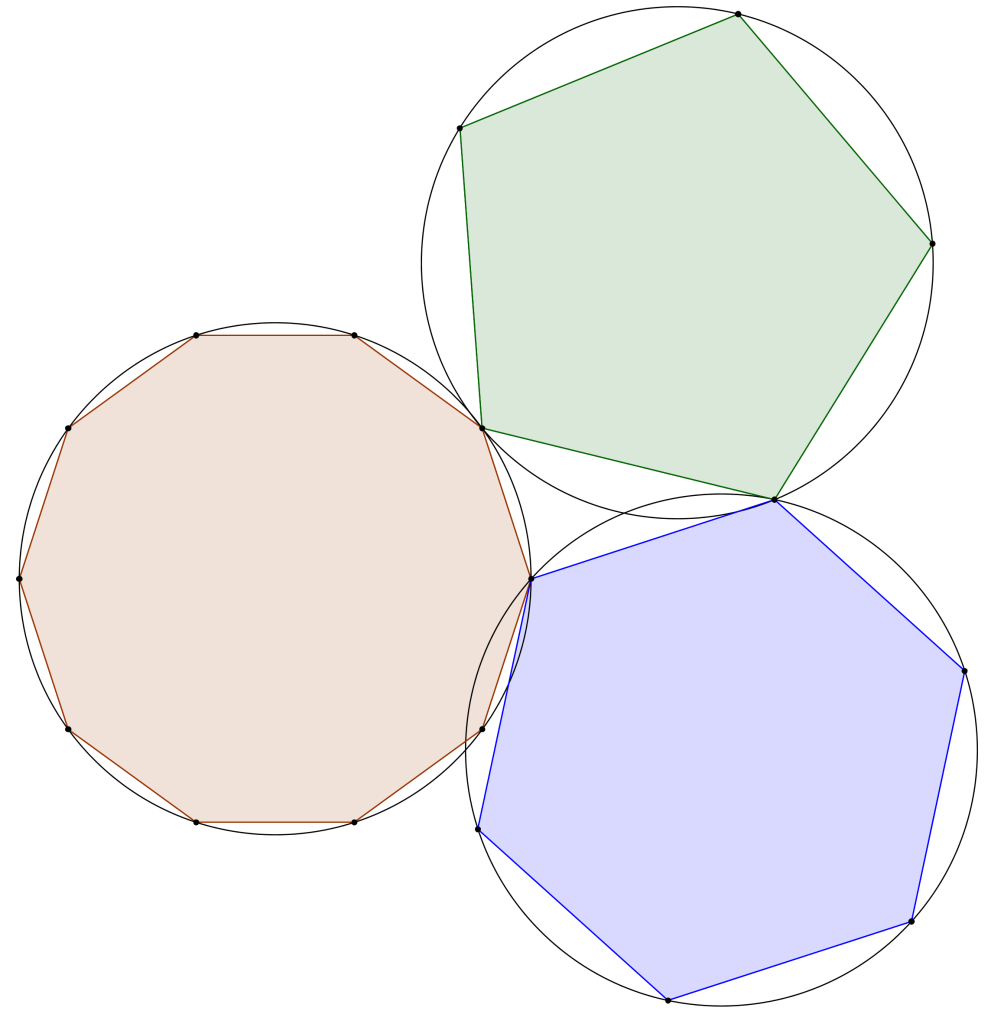
 Dans trois cercles isométriques, on inscrit un pentagone régulier, un hexagone régulier et un décagone régulier. Les côtés de ces trois polygones réguliers forment un triangle rectangle. Ce triangle rectangle est la moitié d’un rectangle d’or.

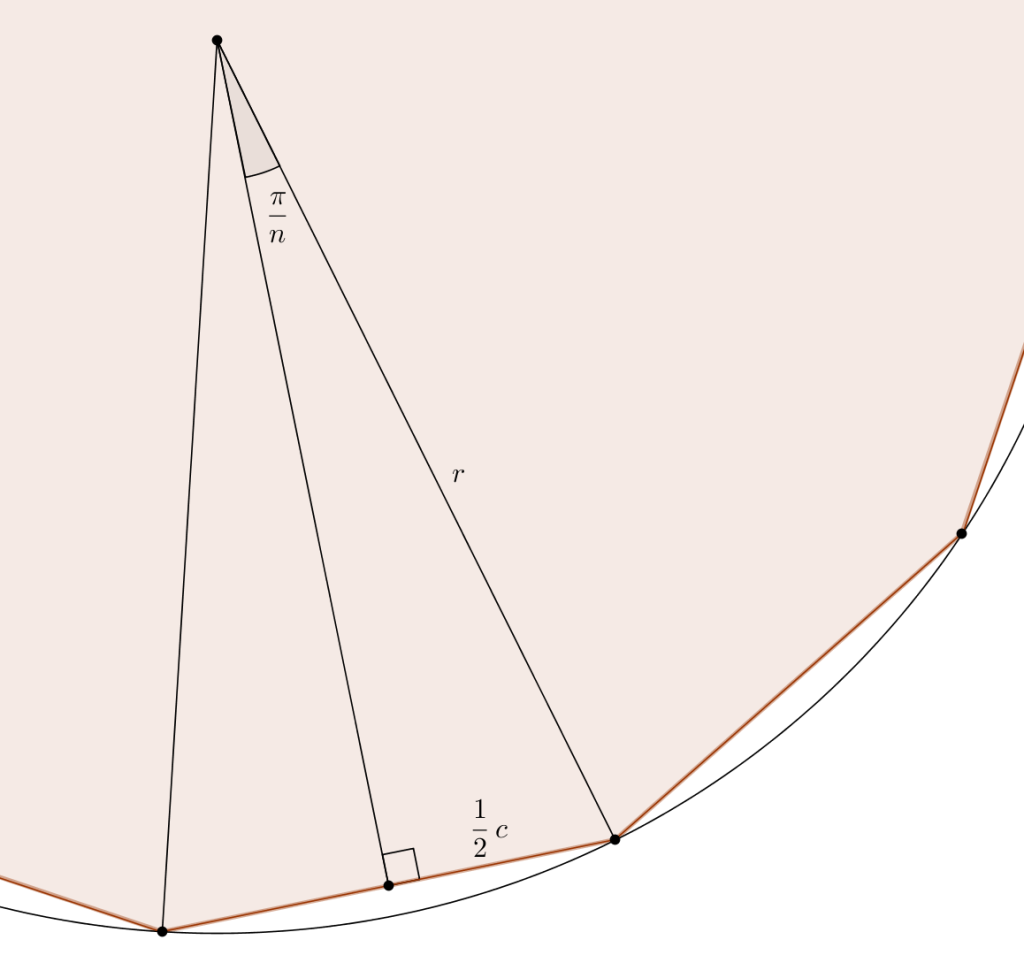
On divise un $n$-gone régulier en $n$ triangles isocèles isométriques. On considère un de ces triangles et on trace la hauteur issue de l’angle de mesure $\frac{2\pi }{n}$. Dans un triangle isocèle, cette hauteur est aussi médiatrice et bissectrice, si bien que l’on forme un triangle rectangle d’hypoténuse $r$, le rayon du cercle, de cathète $\frac{1}{2}c$, la moitié de la mesure du côté du $n$-gone. Cette cathète est opposée à l’angle de $\frac{\pi }{n}$.

Le rapport sinus dans ce triangle rectangle nous donne $$\sin \left(\frac{\pi }{n}\right)=\frac{\frac{1}{2}c}{r}$$ou de manière équivalente, $$c=2r\sin \left(\frac{\pi }{n}\right)$$Ainsi, dans le cas du pentagone régulier, $n=5$ et le côté mesure $$2r\sin \left(\frac{\pi }{5}\right)$$dans le cas de l’hexagone régulier, $n=6$ et le côté mesure $$2r\sin \left(\frac{\pi }{6}\right)$$et enfin dans le cas du décagone régulier, $n=10$ et le côté mesure $$2r\sin \left(\frac{\pi }{10}\right)$$Quelles sont les valeurs de ces sinus ? Dans le cas de l’hexagone, c’est une valeur connue, puisque la mesure du côté de l’hexagone correspond au rayon du cercle (les triangles isocèles sont en fait équilatéraux), et comme on sait que $$\sin \left(\frac{\pi }{6}\right)=\frac{1}{2}$$on trouve sans surprise $$2r\sin \left(\frac{\pi }{6}\right)=2r\cdot \frac{1}{2}=r$$En utilisant un autre résultat, vu ici, on sait que $$\cos \left(\frac{\pi }{5}\right)=\frac{1+\sqrt{5}}{4}$$et en élevant au carré, $${\cos }^2\left(\frac{\pi }{5}\right)=\frac{3+\sqrt{5}}{8}$$En utilisant l’identité fondamentale, $${\sin }^2\left(\alpha \right)+{\cos }^2\left(\alpha \right)=1$$avec ${\displaystyle \alpha =\frac{\pi }{5}}$, on obtient $${\sin }^2\left(\frac{\pi }{5}\right)+{\cos }^2\left(\frac{\pi }{5}\right)=1$$et en remplaçant $${\sin }^2\left(\frac{\pi }{5}\right)+\frac{3+\sqrt{5}}{8}=1$$Cette dernière expression nous donne le carré du sinus, $${\sin }^2\left(\frac{\pi }{5}\right)=\frac{5-\sqrt{5}}{8}$$ou même le sinus, puisque $0<\frac{\pi }{5}<\frac{\pi }{2}$, c’est la racine carrée positive de l’expression précédente $$\sin \left(\frac{\pi }{5}\right)=\sqrt{\frac{5-\sqrt{5}}{8}}$$On fait la même chose avec ${\displaystyle \alpha =\frac{\pi }{10}}$. On a $${\sin }^2\left(\frac{\pi }{10}\right)+{\cos }^2\left(\frac{\pi }{10}\right)=1$$sauf que là, il faut travailler un peu, ou enfin davantage… Avec l’identité $$\sin (\eta +\theta )=\sin \left(\eta \right)\cos \left(\theta \right)+\sin \left(\theta \right)\cos \left(\eta \right)$$on pose $\eta =\theta$ et après quelques étapes algébriques, on obtient la formule du cosinus de l’angle double $$\cos \left(2\eta \right)=2{\cos }^2\left(\eta \right)-1$$Avec ${\displaystyle \eta =\frac{\pi }{10}}$ on obtient $$\cos \left(\frac{\pi }{5}\right)=2{\cos }^2\left(\frac{\pi }{10}\right)-1$$c’est-à-dire $$\frac{1+\sqrt{5}}{4}=2{\cos }^2\left(\frac{\pi }{10}\right)-1$$En additionnant 1 de chaque côté $$\frac{5+\sqrt{5}}{4}=2{\cos }^2\left(\frac{\pi }{10}\right)$$et en divisant par 2, $$\frac{5+\sqrt{5}}{8}={\cos }^2\left(\frac{\pi }{10}\right)$$on obtient la valeur du carré du cosinus. En remplaçant dans l’identité fondamentale,$${\sin }^2\left(\frac{\pi }{10}\right)+{\cos }^2\left(\frac{\pi }{10}\right)=1$$on a $${\sin }^2\left(\frac{\pi }{10}\right)+\frac{5+\sqrt{5}}{8}=1$$et en soustrayant, apparaît la valeur du carré du sinus $${\sin }^2\left(\frac{\pi }{10}\right)=\frac{3-\sqrt{5}}{8}$$Encore une fois, puisque $0<\frac{\pi }{10}<\frac{\pi }{2}$, le sinus est positif $$\sin \left(\frac{\pi }{10}\right)=\sqrt{\frac{3-\sqrt{5}}{8}}$$Il reste à vérifier la relation de Pythagore : si c’est le cas, le triangle est rectangle ! En considérant le plus grand côté, celui du pentagone régulier, comme l’hypoténuse, on pose $${(2r\sin \left(\frac{\pi }{10}\right))}^2+{(2r\sin \left(\frac{\pi }{6}\right))}^2\stackrel{?}{=}{(2r\sin \left(\frac{\pi }{5}\right))}^2$$ou de manière équivalente $$4r^2{\sin }^2\left(\frac{\pi }{10}\right)+4r^2{\sin }^2\left(\frac{\pi }{6}\right)\stackrel{?}{=}4r^2{\sin }^2\left(\frac{\pi }{5}\right)$$

En divisant chaque côté par $4r^2$, $${\sin }^2\left(\frac{\pi }{10}\right)+{\sin }^2\left(\frac{\pi }{6}\right)\stackrel{?}{=}{\sin }^2\left(\frac{\pi }{5}\right)$$Le membre de gauche de l’équation est connu, c’est $$\begin{array}{rl}{\sin }^2\left(\frac{\pi }{10}\right)+{\sin }^2\left(\frac{\pi }{6}\right)& =\frac{3-\sqrt{5}}{8}+\frac{1}{4}\\ \\ & =\frac{5-\sqrt{5}}{8}\\ \\ & ={\sin }^2\left(\frac{\pi }{5}\right)\end{array}$$Le triangle est bien rectangle ! Est-il une moitié de rectangle d’or ? On considère le rapport des mesures des côtés $$\frac{2r\sin \left(\frac{\pi }{6}\right)}{2r\sin \left(\frac{\pi }{10}\right)}=\frac{\sin \left(\frac{\pi }{6}\right)}{\sin \left(\frac{\pi }{10}\right)}$$et ces quelques étapes algébriques simples (mais non moins fastidieuses) $$\begin{array}{rl}\frac{\sin \left(\frac{\pi }{6}\right)}{\sin \left(\frac{\pi }{10}\right)}& =\frac{\frac{1}{2}}{\sqrt{\frac{3-\sqrt{5}}{8}}}\\ \\ & =\frac{\sqrt{\frac{1}{4}}}{\sqrt{\frac{3-\sqrt{5}}{8}}}\\ \\ & =\sqrt{\frac{\frac{1}{4}}{\frac{3-\sqrt{5}}{8}}}\\ \\ & =\sqrt{\frac{\frac{1}{4}\cdot 8}{\frac{3-\sqrt{5}}{8}\cdot 8}}\\ \\ & =\sqrt{\frac{2}{3-\sqrt{5}}}\end{array}$$Suivent encore quelques étapes algébriques de routine, $$\begin{array}{rl}\frac{\sin \left(\frac{\pi }{6}\right)}{\sin \left(\frac{\pi }{10}\right)}& =\sqrt{\frac{2}{3-\sqrt{5}}}\\ \\ & =\sqrt{\frac{2(3+\sqrt{5})}{(3-\sqrt{5})(3+\sqrt{5})}}\\ \\ & =\sqrt{\frac{2(3+\sqrt{5})}{4}}\\ \\ & =\sqrt{\frac{3+\sqrt{5}}{2}}\end{array}$$Il suffit enfin de se rendre compte que l’expression dans la grande racine carrée est un carré $$\begin{array}{rl}\frac{\sin \left(\frac{\pi }{6}\right)}{\sin \left(\frac{\pi }{10}\right)}& =\sqrt{\frac{3+\sqrt{5}}{2}}\\ \\ & =\sqrt{\frac{6+2\sqrt{5}}{4}}\\ \\ & =\sqrt{\frac{1^2+2\sqrt{5}+{\left(\sqrt{5}\right)}^2}{4}}\\ \\ & =\sqrt{\frac{{(1+\sqrt{5})}^2}{4}}\\ \\ & =\frac{1+\sqrt{5}}{2}\end{array}$$pour qu’apparaisse le nombre d’or !

Euclide, vieille branche !

En suivant le lien sur Futility Closet, on découvre que l’auteur de l’image de Wikimedia Commons est nul autre que David Eppstein et que l’image est intitulée : Euclid XIII.10. Diantre ! Érudits, à vos Éléments ! (Heureusement, je possède une copie peu dispendieuse, en anglais.) Comment Euclide s’y prend-t-il ? C’est sans surprise qu’il utilise son arme favorite… des triangles semblables !

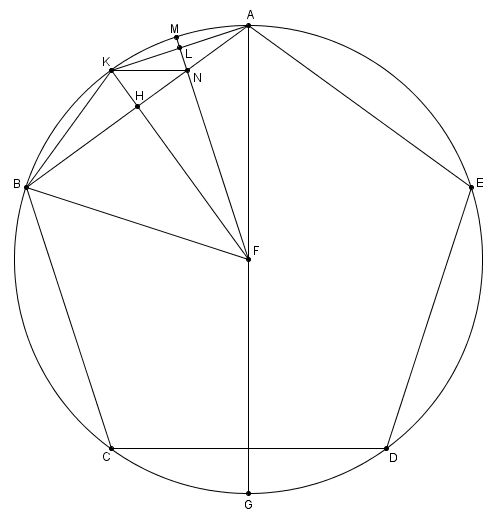
Il inscrit d’abord le pentagone régulier $ABCDE$ dans un cercle de centre $F$. Il trace un diamètre $\overline{AG}$. Il trace $\overline{FB}$ et $\overline{FK}$, perpendiculaire à $\overline{AB}$, coupant $\overline{AB}$ en $H$. Il trace ensuite $\overline{AK}$ et $\overline{KB}$. Enfin, il trace la perpendiculaire à $\overline{AK}$ passant par $F$, coupant $\overline{AB}$ en $N$, $\overline{AK}$ en $L$ et le cercle en $M$.

Il remarque d’abord que puisque $\overline{AG}$ est un diamètre, $\stackrel{{\displaystyle ⌢}}{CG}\cong \stackrel{{\displaystyle ⌢}}{GD}$. Puisque la corde $\overline{CD}$ est le côté d’un pentagone régulier, les cordes $\overline{CG}$ et $\overline{GD}$ sont  les côtés d’un décagone régulier.

Le segment $\overline{FK}$ étant perpendiculaire à $\overline{AB}$ et $\overline{FB}\cong \overline{FA}$, on trouve (par I.26) que $\mathrm{\angle }AFK\cong \mathrm{\angle }BFK$. Comme $\overline{AB}$ est le côté d’un pentagone régulier, cela implique que $\overline{BK}$ et $\overline{KA}$ sont aussi les côtés d’un décagone régulier.

De la même manière, $\overline{FM}$ étant perpendiculaire à $\overline{AK}$, on observe que $\overline{AL}\cong \overline{LK}$ et $\stackrel{{\displaystyle ⌢}}{AM}\cong \stackrel{{\displaystyle ⌢}}{MK}$.

Par la suite Euclide s’attarde à montrer deux choses : les triangles $ABF$ et $FBN$ sont semblables, tout comme les triangles $ABK$ et $AKN$. On a $$\begin{array}{rl}2m\stackrel{{\displaystyle ⌢}}{CG}& =m\stackrel{{\displaystyle ⌢}}{CD}\\ \\ & =m\stackrel{{\displaystyle ⌢}}{AB}\\ \\ & =2m\stackrel{{\displaystyle ⌢}}{BK}\end{array}$$c’est-à-dire que $$\begin{array}{rl}m\stackrel{{\displaystyle ⌢}}{CG}=m\stackrel{{\displaystyle ⌢}}{BK}& =m\stackrel{{\displaystyle ⌢}}{AK}\\ \\ & =2m\stackrel{{\displaystyle ⌢}}{KM}\end{array}$$et $$m\stackrel{{\displaystyle ⌢}}{CB}=2m\stackrel{{\displaystyle ⌢}}{BK}$$En additionnant, on a $$m\stackrel{{\displaystyle ⌢}}{BCG}=2m\stackrel{{\displaystyle ⌢}}{BKM}$$ou, en considérant les angles au centre, $$m\mathrm{\angle }BFG=2m\mathrm{\angle }BFN$$Sauf que $$m\mathrm{\angle }BFG=2m\mathrm{\angle }FAB$$puisque l’angle $FAB$ inscrit intercepte le même arc que l’angle au centre $BFG$. En substituant, on trouve $$m\mathrm{\angle }FAB=m\mathrm{\angle }BFN$$Ainsi, les triangles $ABF$ et $FBN$ on un angle en commun, $\mathrm{\angle }ABF$, et des angles isométriques $$\mathrm{\angle }FAB\cong \mathrm{\angle }BFN$$ce qui fait que les triangles sont semblables ! $$△ABF\sim △FBN$$D’autre part, puisque $\overline{AL}\cong \overline{LK}$, et que les angles en $L$ sont des angles droits, on trouve que $$\overline{AN}\cong \overline{NK}$$ainsi que, comme dans un triangle isocèle les angles opposés aux côtés isométriques sont isométriques, $$\begin{array}{rl}\mathrm{\angle }NKA& \cong \mathrm{\angle }NAK\\ \\ & \cong \mathrm{\angle }KBA\end{array}$$Ainsi, les triangles $ABK$ et $AKN$ ont un angle en commun, $\mathrm{\angle }NAK$, et des angles isométriques $$\mathrm{\angle }ABK\cong \mathrm{\angle }AKN$$Les triangles sont semblables $$△ABK\sim △AKN$$Maintenant, puisque $△ABF\sim △FBN$, on pose la proportion$$\frac{m\overline{AB}}{m\overline{BF}}=\frac{m\overline{BF}}{m\overline{BN}}$$ou, de manière équivalente,$$m\overline{AB}\cdot m\overline{BN}={\left(m\overline{BF}\right)}^2$$En utilisant l’autre similitude, $△ABK\sim △AKN$, on trouve $$\frac{m\overline{BA}}{m\overline{AK}}=\frac{m\overline{AK}}{m\overline{AN}}$$ou, de manière équivalente,$$m\overline{BA}\cdot m\overline{AN}={\left(m\overline{AK}\right)}^2$$Ainsi, en additionnant les égalités,$$m\overline{AB}\cdot m\overline{BN}+m\overline{BA}\cdot m\overline{AN}={\left(m\overline{BF}\right)}^2+{\left(m\overline{AK}\right)}^2$$c’est-à-dire $$\begin{array}{rl}m\overline{AB}\cdot (m\overline{AN}+m\overline{BN})& ={\left(m\overline{BF}\right)}^2+{\left(m\overline{AK}\right)}^2\\ {\left(m\overline{AB}\right)}^2& ={\left(m\overline{BF}\right)}^2+{\left(m\overline{AK}\right)}^2\end{array}$$

On vérifie la relation de Pythagore, avec $AB$ le côté d’un pentagone, $BF$ d’un hexagone (c’est le rayon du cercle) et $AK$ d’un décagone.