Grâce à la relation de Pythagore et à quelques triangles rectangles bien choisis, il est facile de calculer les valeurs exactes de certains rapports trigonométriques. Les classiques \[\sin(30^{\circ}) = \cos(60^{\circ}) = \frac{1}{2}\]ou \[\sin(45^{\circ}) = \cos(45^{\circ}) = \frac{\sqrt{2}}{2}\]ou encore \[\sin(60^{\circ}) = \cos(30^{\circ}) = \frac{\sqrt{3}}{2}\]peuvent être trouvés de cette façon. Puis, avec les formules d’addition d’angles et d’angles doubles, on peut trouver d’autres valeurs exactes. Par exemple, en se rappelant que \[\sin(\alpha + \beta) = \sin(\alpha)\cos(\beta)+\sin(\beta)\cos(\alpha)\]on peut trouver \[\sin(30^{\circ} + 45^{\circ})=\sin(30^{\circ})\cos(45^{\circ})+\sin(45^{\circ})\cos(30^{\circ})\]Et en remplaçant par ce qui est connu, on obtient \[\sin(75^{\circ}) = \frac{1}{2}\cdot \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2}\]ce qui fait \[\sin(75^{\circ})= \frac{\sqrt{2}}{4}+ \frac{\sqrt{6}}{4}\]ou si on préfère \begin{align*}\sin(75^{\circ}) &= \frac{\sqrt{2} + \sqrt{6}}{4} \\ \\ &=\frac{\sqrt{2}\left(1+\sqrt{3}\right)}{4}\end{align*}Ou bien, en se rappelant que \[\cos(2\alpha) = 2\cos^{2}(\alpha)-1\]on trouve \[\cos(2\cdot 15^{\circ}) = 2\cos^{2}(15^{\circ})-1\]ce qui fait \[\cos(30^{\circ}) = 2\cos^{2}(15^{\circ})-1\]En remplaçant la valeur du cosinus connue, on obtient \[\frac{\sqrt{3}}{2}=2\cos^{2}(15^{\circ})-1\]On additionne \(1\) de chaque côté \[\frac{\sqrt{3}}{2} + 1 = 2\cos^{2}(15^{\circ})\]ce qui fait \[\frac{\sqrt{3}}{2} + \frac{2}{2}=2\cos^{2}(15^{\circ})\]et donc \[\frac{\sqrt{3}+2}{2}= 2\cos^{2}(15^{\circ})\]Puis en divisant chaque côté de l’équation par \(2\) \[\frac{\sqrt{3}+2}{4} = \cos^{2}(15^{\circ})\]Il suffit enfin d’extraire la racine carrée de chaque côté de l’équation (on note que \(\cos(15^{\circ})\) est positif) \[\sqrt{\frac{\sqrt{3}+2}{4}} = \cos(15^{\circ})\]ce qui fait \[\frac{\sqrt{\sqrt{3}+2}}{\sqrt{4}} = \cos(15^{\circ})\]et donc plus simplement \[\frac{\sqrt{\sqrt{3}+2}}{2} = \cos(15^{\circ})\]Et comme \[\sin(75^{\circ})=\cos(15^{\circ})\]on obtient ce joli résultat \[\frac{\sqrt{6}+\sqrt{2}}{4} = \frac{\sqrt{\sqrt{3}+2}}{2}\] \[\frac{\sqrt{6}+\sqrt{2}}{4} = \frac{2\sqrt{\sqrt{3}+2}}{4}\] \[\sqrt{6} +\sqrt{2}= 2\sqrt{\sqrt{3}+2}\]
Bon. Tout cela reste cependant bien peu spectaculaire. Voici un résultat différent qui, en général, ne manque pas d’impressionner les étudiants. Trouvons la valeur exacte de \(\cos(36^{\circ})\). Exit les triangles rectangles. Nous allons considérer le triangle isocèle suivant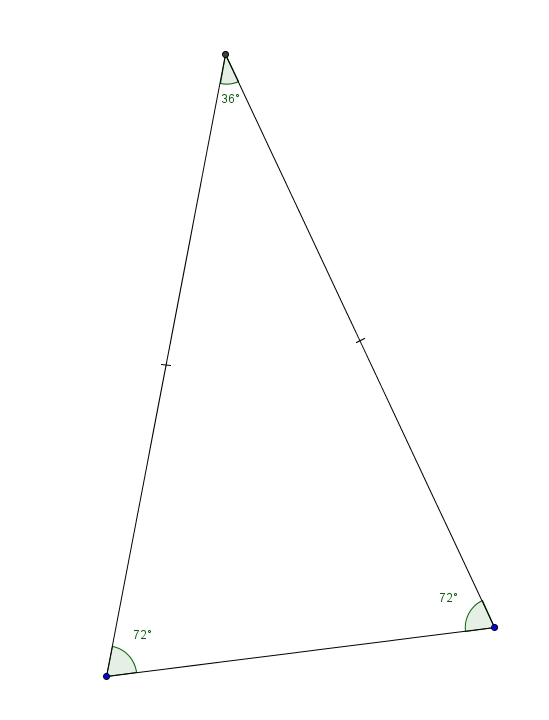 On appelle ce triangle le triangle d’or. Si on trace la bissectrice d’un des angles de \(72^{\circ}\), on obtient un nouveau triangle isocèle semblable au premier (cas de similitude AA). On peut répéter le processus indéfiniment. Ceux qui connaissent le rectangle d’or y voient l’analogie.
On appelle ce triangle le triangle d’or. Si on trace la bissectrice d’un des angles de \(72^{\circ}\), on obtient un nouveau triangle isocèle semblable au premier (cas de similitude AA). On peut répéter le processus indéfiniment. Ceux qui connaissent le rectangle d’or y voient l’analogie.
Traçons, justement, une de ces bissectrices. On obtient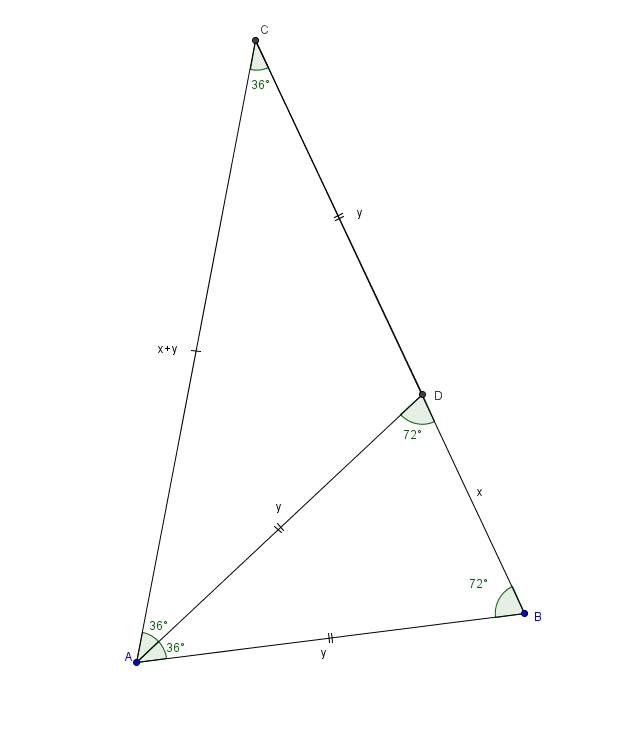
Le triangle \(ABD\) est semblable au triangle \(ABC\) par AA. Le triangle \(ABD\) est isocèle. Si \(\overline{AB}\) mesure \(y\), alors \(\overline{AD}\) aussi puisque ce sont les côtés isométriques du triangle isocèle. Mais il y a en un troisième, triangle isocèle, bien qu’il ne soit pas semblable aux deux autres. C’est le triangle \(ADC\) (observez la paire d’angles de \(36^{\circ}\)). On trouve ainsi que la mesure de \(\overline{DC}\) est aussi égale à \(y\). En posant la mesure de \(\overline{BD}\) égale à \(x\), on trouve que la mesure de \(\overline{BC}\) (et donc aussi de \(\overline{AC}\)) est égale à \(x+y\). On peut établir la proportion suivante en associant correctement les côtés homologues dans les deux triangles semblables \[\frac{m\overline{BD}}{m\overline{AB}} = \frac{m\overline{AB}}{m\overline{BC}}\] ou plus simplement \[\frac{x}{y} = \frac{y}{x+y}\]En effectuant le produit croisé, on obtient \[x^{2}+xy = y^{2}\]On divise ensuite chaque côté par \(x^{2}\) \[\frac{x^{2}}{x^{2}}+\frac{xy}{x^{2}} = \frac{y^{2}}{x^{2}}\]ce qui fait \[1 + \frac{y}{x} = \left(\frac{y}{x}\right)^{2}\]On obtient ainsi un polynôme du deuxième degré en \(\frac{y}{x}\) \[\left(\frac{y}{x}\right)^{2}-\frac{y}{x}-1=0\]Avec la formule quadratique, on trouve \[\frac{y}{x}=\frac{-(-1)\pm\sqrt{(-1)^{2}-4\cdot 1\cdot (-1)}}{2\cdot 1}\]Comme \(\frac{y}{x}\) est un rapport de mesures positives, on ne retient que la valeur positive pour \(\frac{y}{x}\) \[\frac{y}{x}=\frac{1+\sqrt{1+4}}{2}\]ce qui fait \[\frac{y}{x}= \frac{1+\sqrt{5}}{2}\]On reconnait d’ailleurs le nombre d’or. Pour des raisons à ce moment loin d’être apparentes, on fait deux choses : d’abord on inverse et puis on élève au carré. On obtient dans un premier temps \[\frac{x}{y} = \frac{2}{1+\sqrt{5}}\]En rationalisant le dénominateur on obtient \begin{align*}\frac{x}{y}&=\frac{2}{1+\sqrt{5}} \\ \\ &=\frac{2}{1+\sqrt{5}} \cdot \frac{1-\sqrt{5}}{1-\sqrt{5}} \\ \\ &= \frac{2\left(1-\sqrt{5}\right)}{-4}\end{align*}ce qui fait en simplifiant le dénominateur \[\frac{x}{y} = \frac{-1+\sqrt{5}}{2}\]Sitôt ce résultat obtenu, on élève au carré \[\left(\frac{x}{y}\right)^{2}=\left(\frac{-1+\sqrt{5}}{2}\right)^{2}\]ce qui est équivalent à \[\left(\frac{x}{y}\right)^{2}=\frac{\left(-1+\sqrt{5}\right)^{2}}{2^{2}}\]En développant \[\left(\frac{x}{y}\right)^{2}= \frac{1-2\sqrt{5}+5}{4}\]et en regroupant les termes semblables \[\left(\frac{x}{y}\right)^{2}= \frac{6-2\sqrt{5}}{4}\]Finalement, en simplifiant la fraction, on obtient \[\left(\frac{x}{y}\right)^{2}=\frac{3-\sqrt{5}}{2}\]Considérons maintenant l’angle BAD de 36° dans le triangle BAD. En utilisant la loi des cosinus, on peut écrire \[x^{2}=y^{2}+y^{2}-2\cdot y\cdot y \cdot \cos(36^{\circ})\]En simplifiant le membre de droite on obtient \[x^{2}=2y^{2}-2y^{2}\cos(36^{\circ})\]On effectue d’abord la mise en évidence du carré de \(y\) à droite \[x^{2}=y^{2}\left(2-2\cos(36^{\circ})\right)\]puis on divise chaque côté par ce même carré de \(y^{2}\) \[\frac{x^{2}}{y^{2}}=2-2\cos(36^{\circ})\]Il nous suffit donc d’écrire \[\left(\frac{x}{y}\right)^{2}=2-2\cos(36^{\circ})\]pour comprendre la peine qu’on s’était donnée pour trouver \[\left(\frac{x}{y}\right)^{2}=\frac{3-\sqrt{5}}{2}\]On obtient donc \[\frac{3-\sqrt{5}}{2}=2-2\cos(36^{\circ})\]Il suffit maintenant d’isoler sans trop de mal le cosinus. On divise chaque côté par \(2\) \[\frac{3-\sqrt{5}}{4}=1-1\cos(36^{\circ})\]On soustrait ensuite \(1\) de chaque côté \[\frac{3-\sqrt{5}}{4}-1=-\cos(36^{\circ})\]ce qui fait \[\frac{3-\sqrt{5}}{4}-\frac{4}{4} = -\cos(36^{\circ})\]et donc en effectuant la soustraction \[\frac{-1-\sqrt{5}}{4} = -\cos(36^{\circ})\]On multiplie enfin chaque côté de l’égalité par \(-1\) \[\frac{1+\sqrt{5}}{4}=\cos(36^{\circ})\]Voilà ! La valeur exacte du cosinus de \(36^{\circ}\).
Je jongle présentement avec les notions de preuves et les types de raisonnements (abductif, inductif et déductif) et cette superbe démonstration cadre à merveille dans mes réflexions. Merci beaucoup.
Je vous en prie !
Bonne journée !