Il existe des expressions simples pour les mesures des bissectrices et des médianes dans un triangle qui ne font intervenir que les mesures des côtés.
La mesure d’une bissectrice dans un triangle
Petite référence au tout premier billet de ce blogue sur le Théorème de Stewart. C’était en novembre 2009. Ce blogue vient donc de célébrer son 13e anniversaire. Misère que le temps passe vite !
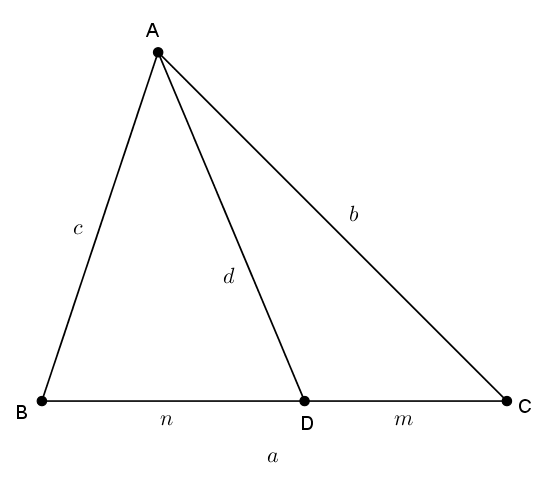
Dans un triangle \(ABC\) avec, comme d’habitude, \(m\overline{BC} = a\), \(m\overline{AC} = b\) et \(m\overline{AB} = c\), on trace une cévienne \(AD\) qui coupe \(\overline{BC}\) dans un rapport \(n:m\). En d’autres mots, \(m\overline{BD} =n\), \(m\overline{DC} = m\) et donc \(a = m + n\). Le théorème de Stewart nous dit que \[a(d^{2}+mn) = nb^{2}+mc^{2}\]
On utilisera aussi un autre théorème, cette fois-ci vu ici en 2010 : le théorème de la bissectrice dans un triangle. Si la cévienne \(AD\) est une bissectrice, alors elle partage le côté opposé proportionnellement aux côtés de l’angle, c’est-à-dire qu’on a en plus \[\frac{b}{m} = \frac{c}{n}\]On aura d’abord besoin d’exprimer ce rapport de plusieurs autres façons équivalentes. Ainsi, on a également\[\frac{b}{c} = \frac{m}{n}\]Cela nous permet d’écrire \begin{align*}\frac{b}{c}&=\frac{m}{n} \\ \\ \frac{b}{c} + 1 &= \frac{m}{n} + 1 \\ \\ \frac{b}{c} + \frac{c}{c} &= \frac{m}{n} + \frac{n}{n} \\ \\ \frac{b+c}{c} &= \frac{m+n}{n}\end{align*}De manière équivalente, on a aussi : \[\frac{c}{b+c} = \frac{n}{m+n}\]En partant plutôt du rapport inverse, \[\frac{c}{b} = \frac{n}{m}\]on obtient, avec une démarche similaire,\[\frac{b+c}{b}= \frac{m+n}{m}\]ou \[\frac{b}{b+c} = \frac{m}{m+n}\]En partant du théorème de Stewart, il sera possible de remplacer \(m\) et \(n\) par des expressions ne contenant que \(a\), \(b\) ou \(c\). On isole d’abord \(d^{2}\) dans \[a(d^{2}+mn) = nb^{2}+mc^{2}\]ce qui fait \begin{align*}d^{2}+mn &= \frac{nb^{2}+mc^{2}}{a} \\ \\ &= \frac{nb^{2}+mc^{2}}{a}-mn \\ \\ &= b^{2}\cdot \frac{n}{a} + c^{2}\cdot \frac{m}{a}-mn\end{align*}La première astuce est de remplacer \(a = m+n\) pour obtenir \begin{align*}d^{2}&=b^{2}\cdot \frac{n}{m+n} + c^{2}\cdot \frac{m}{m+n}-mn \\ \\ &=b^{2}\cdot \frac{c}{b+c} + c^{2}\cdot \frac{b}{b+c}-mn \\ \\ &= \frac{b^{2}c + c^{2}b}{b+c}-mn\\ \\ &=\frac{bc(b+c)}{b+c}-mn \\ \\ &=bc-mn\end{align*}Pas mal ! Comment se débarrasser des \(m\) et \(n\) du dernier terme ? C’est plus subtil. On multiple ce dernier terme par \(\frac{a^{2}}{a^{2}}\). \begin{align*}d^{2}&=bc-mn \\ \\ &= bc-\frac{mna^{2}}{a^{2}} \\ \\ &=bc-\frac{m}{a}\cdot\frac{n}{a}\cdot a^{2} \\ \\ &=bc-\frac{m}{m+n}\cdot \frac{n}{m+n}\cdot a^{2} \\ \\ &=bc-\frac{b}{b+c}\cdot\frac{c}{b+c}\cdot a^{2} \\ \\ &=bc-\frac{bca^{2}}{(b+c)^2} \\ \\ &=bc\left(1-\frac{a^2}{(b+c)^2}\right)\end{align*} Voilà ! On trouve \[d = \sqrt{bc\left(1-\frac{a^{2}}{(b+c)^{2}}\right)}\]ou si on préfère \[d = \sqrt{bc\left(1-\left(\frac{a}{b+c}\right)^{2}\right)}\]
La mesure d’une médiane
Le théorème de Stewart nous donne aussi une expression pour la longueur des médianes. Il y a moins de travail à faire dans ce cas-ci car si la cévienne \(AD\) est une médiane, alors \[m = n = \frac{a}{2}\]
En partant de \[d^{2}= \frac{nb^{2}+mc^{2}}{a}-mn\]on obtient \begin{align*}d^{2}&=\frac{\frac{a}{2}\cdot b^{2}+ \frac{a}{2}\cdot c^{2}}{a}-\frac{a}{2}\cdot \frac{a}{2} \\ \\ &= \frac{b^{2}+c^{2}}{2}-\frac{a^{2}}{4}\end{align*}ce qui fait \[d = \sqrt{\frac{b^{2}+c^{2}}{2}-\frac{a^{2}}{4}}\]ou, de manière équivalente, \begin{align*}d &= \sqrt{\frac{2(b^{2}+c^{2})}{4}-\frac{a^{2}}{4}} \\ \\ &= \sqrt{\frac{2(b^{2}+c^{2})-a^{2}}{4}} \\ \\ &= \frac{\sqrt{2(b^{2}+c^{2})-a^{2}}}{2}\end{align*}