Bon bon bon… peut-être que je lis un peu trop de Marty Ross ces temps-ci, mais ce dernier billet m’en inspire un autre. Un peu facile j’en conviens, mais ce qui suit provient de la chaîne Youtube du très sérieux Ministère de l’Éducation, et les commentaires sous la vidéo sont désactivés, ça devrait donc être suffisant pour me dédouaner.
On y trouve une liste de lecture dont le titre est « Mathématique ». Une occasion en or pour parfaire ma formation. Je ne sais pas si je serai en mesure de comptabiliser cela dans mes 30 heures d’« activités de formation continue » obligatoires, mais bon.
Les vidéos sur les conjectures ont retenu mon attention. En toute franchise, dans l’ensemble c’est bien.
La dernière partie de la vidéo est consacrée à la création de situations de conjectures appropriées ou la modification de situations déjà existantes.

Dans la vidéo, on explique que des enseignants ont rédigés des situations qui servent d’exemples dans une formation antérieure.

Or, \[\arctan\left(\frac{10\div 2}{8}\right) \approx 32^{\circ}\]ce qui n’est pas égal à \(36^{\circ}\) comme ça devrait l’être dans un pentagone régulier (voir ici au besoin).
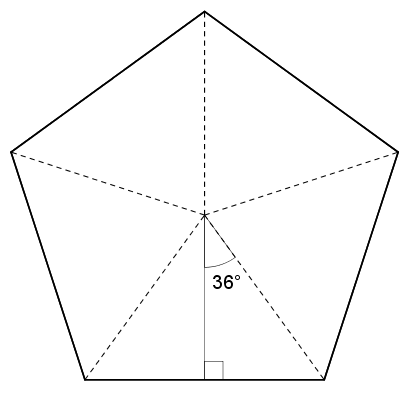
Je ne crois pas non plus à une erreur due à l’arrondissement à l’entier le plus près, car dans ce cas on aurait plutôt eu respectivement 10 cm et 7 cm ou 12 cm et 8 cm. Ce pentagone régulier n’existe tout simplement pas. L’idée n’est pas mauvaise, mais au temps de Géogébra et tout le reste, je ne comprends pas que ces erreurs surviennent encore. De toute façon, c’est au deuxième point où le bât blesse.

Un heptagone régulier et un pentagone régulier dont les mesures de côtés et des apothèmes sont les mêmes ? Je ne suis pas didacticien, mais il y a certainement une dissociation dans les têtes des auteurs de ces questions entre l’expression algébrique et les variables \[A = \frac{c \cdot a \cdot n}{2}\]et les concepts géométriques et grandeurs qu’elles représentent. S’en suivent des manipulations algébriques (ou arithmétiques dans ce cas-ci) dépourvues de sens. Je suis un peu surpris et déçu que les responsables des programmes d’études en mathématique n’aient pas identifié cette erreur.
La diapositive suivante ne me rassure guère.

En supposant que le pentagone soit toujours régulier (puisqu’on parle d’apothème), on pourrait croire qu’on cherche respectivement les réponses « L’aire quadruple » et « Faux, l’aire quadruple » pour les deux premiers points. Cependant le troisième point me fait croire qu’on s’attendait plutôt à ce que l’élève réponde « L’aire double » et « Vrai » aux deux premiers points… pour ensuite répondre : « Faux, l’aire quadruple » au troisième. Mais bon, ne nous perdons pas en conjectures…