On considère un cercle, disons, de rayon \(1\).

On circonscrit un triangle équilatéral.

Puis un cercle.

On circonscrit ensuite un carré.

Puis à nouveau un cercle.

On circonscrit un pentagone régulier.
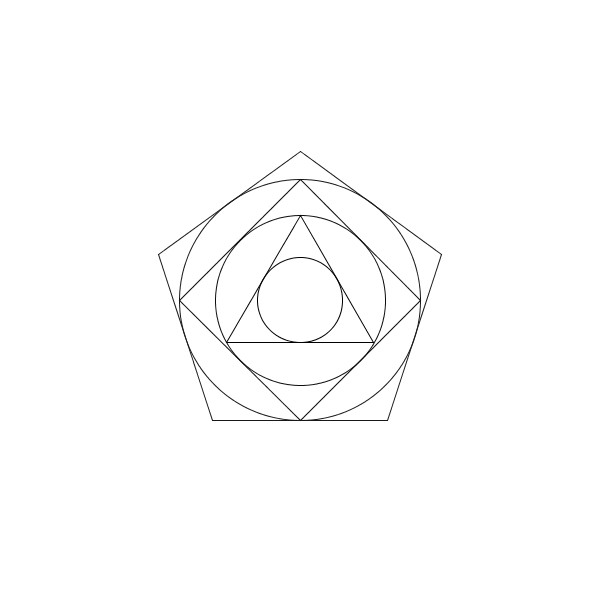
Puis un cercle, encore.

Et on continue de la sorte, en circonscrivant toujours un polygone régulier qui comporte un côté de plus que celui de l’étape précédente, suivi d’un cercle.
Clairement, en continuant le processus, le bons sens nous dit que la figure résultante n’aura pas de borne ! Que les rayons des cercles circonscrits tendent vers \(\infty\).

Vraiment ? Qu’en est-il réellement ?
On considère à nouveau un cercle de rayon \(1\).

Au lieu de circonscrire, cette-fois, on inscrit un triangle équilatéral. Puis dans le triangle, un cercle.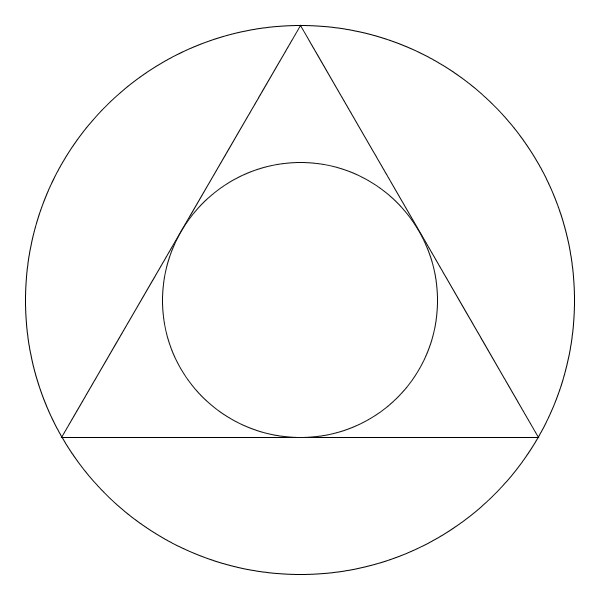
Puis dans le cercle, on inscrit un carré et, dans le carré, un cercle à nouveau.
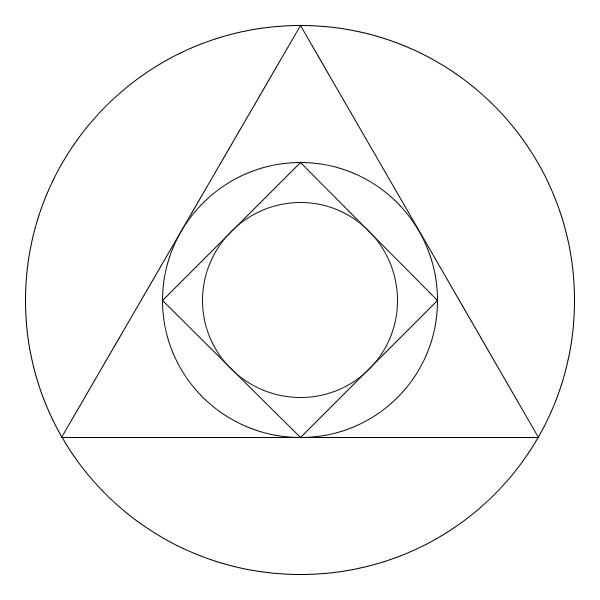
Puis un pentagone régulier et dans le pentagone, un cercle, encore.
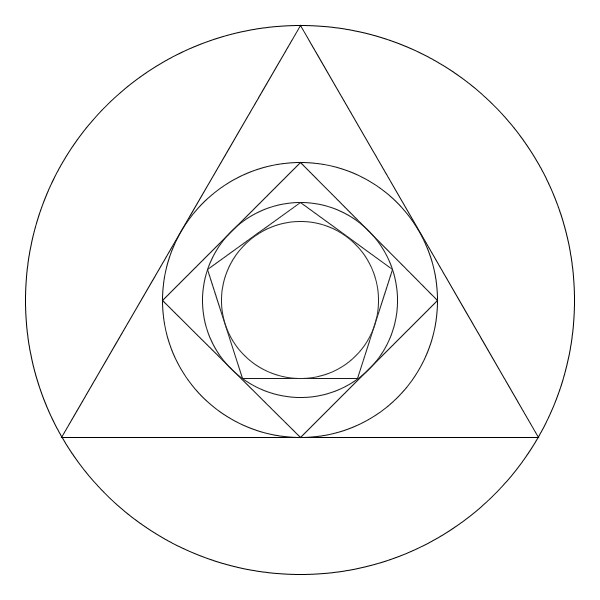
On continue ainsi en inscrivant toujours un cercle et un polygone régulier qui comporte un côté de plus qu’à l’étape précédente. Clairement, le bon sens nous dit que les rayons des cercles successifs tendent vers \(0\) et convergent vers le centre de la figure.
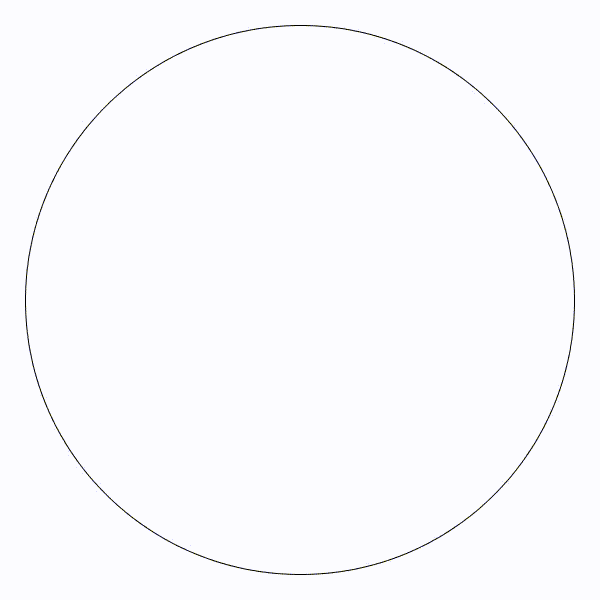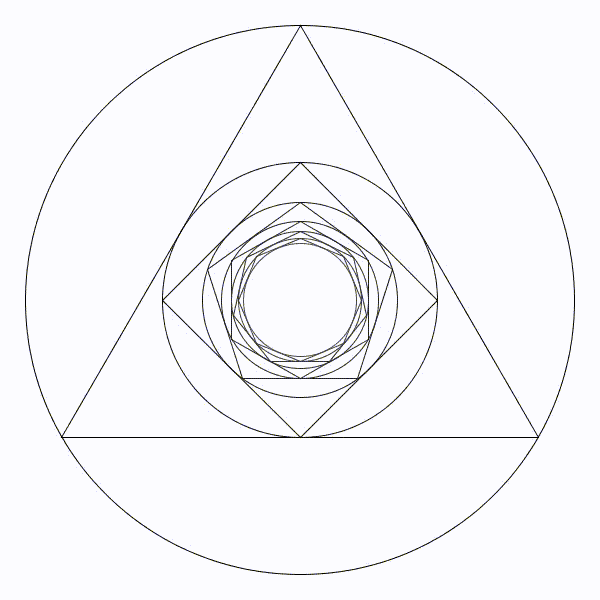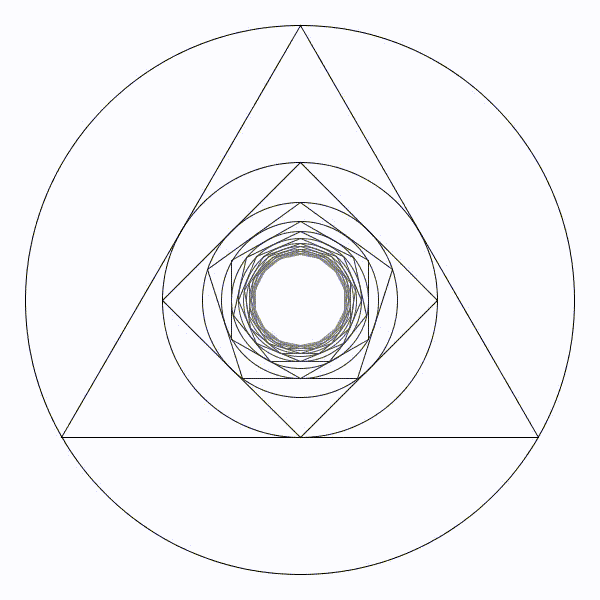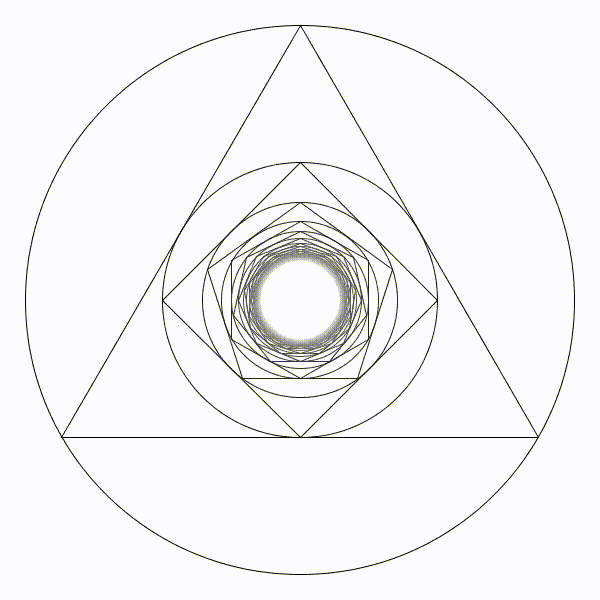
Vraiment ? Qu’en est-il réellement ?
La rigueur mathématique vient à notre rescousse car dans ces cas-ci, notre « bon sens » nous induit en erreur. Dans les deux cas, les rayons des cercles tendent vers des limites qui ne sont ni \(\infty\), ni \(0\). Dans le premier cas, on peut tracer un cercle extérieur à la figure, dont le rayon est un peu moins de \(8,\!7\), et qui ne sera jamais atteint. Dans le deuxième cas, on peut tracer un cercle à l’intérieur de la figure, dont le rayon est environ \(0,\!11\), et qui ne sera jamais atteint. N’est-ce pas à la fois surprenant et remarquable ?
Les deux exemples sont tirés du livre Mathematics and the Imagination, d’Edward Kasner & James Newman[0]. C’est dans ce livre que Kasner introduit le mot « googol » pour le nombre \(10^{100}\) et googolplex pour le nombre \(10^{\text{googol}}\).
A googol is this number which one of the children in the kindergarten wrote on the blackboard: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
At the same time that he suggested “googol” he gave a name for a still larger number: “googolplex.” […] The googolplex then, is a specific finite number, with so many zeros after the 1 that the number of zeros is a googol. A googolplex is much bigger than a googol, much bigger even than a googol times a googol. A googol times a googol would be 1 with 200 zeros, whereas a googolplex is 1 with a googol of zeros. You will get some idea of the size of this very large but finite number from the fact that there would not be enough room to write it, if you went to the farthest star, touring all the nebulae and putting down zeros every inch of the way.
Pour les irréductibles, voir ceci : http://www.googolplexwrittenout.com/
À la limite
Considérons d’abord le premier cas. À une étape quelconque, on circonscrit un polygone à \(n\) côtés à un cercle \(c\) de rayon \(r\). Le cercle \(C\) de rayon \(R\), lui, est circonscrit au polygone. Disons que l’angle au centre du polygone est \(\theta\).
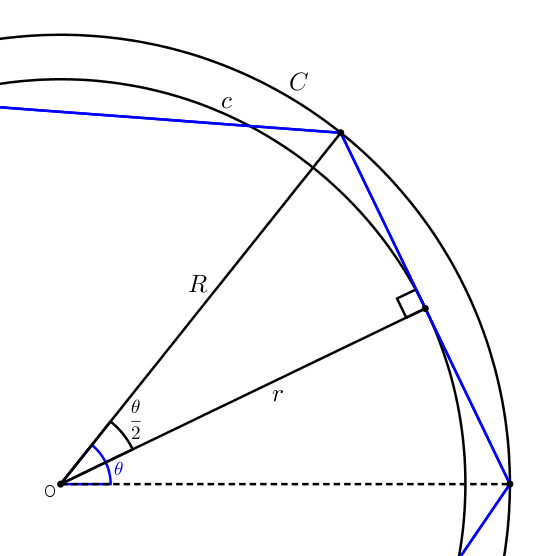
On a \[\cos\left(\frac{\theta}{2}\right) = \frac{r}{R}\]ou de manière équivalente, \[R = \frac{r}{\cos\left(\frac{\theta}{2}\right)}\]ou encore, \[R = \sec\left(\frac{\theta}{2}\right)r\]Puisque le polygone régulier comporte \(n\) côtés, on trouve que \[\theta = \frac{2\pi}{n}\]ce qui donne \begin{align*}R&=\sec\left(\frac{\theta}{2}\right)r \\ \\ &=\sec\left(\frac{\frac{2\pi}{n}}{2}\right)r \\ \\ &= \sec\left(\frac{\pi}{n}\right)r\end{align*}
Puisque le rayon du cercle de départ est 1, le rayon du premier cercle circonscrit est \[R_1 = \sec\left(\frac{\pi}{3}\right)\]le rayon du deuxième cercle circonscrit est \[R_2 = \sec\left(\frac{\pi}{3}\right)\sec\left(\frac{\pi}{4}\right)\]le rayon du troisième cercle circonscrit est \[R_3 = \sec\left(\frac{\pi}{3}\right)\sec\left(\frac{\pi}{4}\right)\sec\left(\frac{\pi}{5}\right)\]et le rayon du \(n^{\text{e}}\) cercle est \[R_n = \sec\left(\frac{\pi}{3}\right)\sec\left(\frac{\pi}{4}\right)\sec\left(\frac{\pi}{5}\right)\ \cdot \ \dots \ \cdot \ \sec\left(\frac{\pi}{n+2}\right)\]On cherche la limite suivante \[R = \lim_{n\to \infty}\sec\left(\frac{\pi}{3}\right)\sec\left(\frac{\pi}{4}\right)\sec\left(\frac{\pi}{5}\right)\ \cdot \ \dots \ \cdot \ \sec\left(\frac{\pi}{n}\right)\]ou, plus informellement, \[R = \sec\left(\frac{\pi}{3}\right)\sec\left(\frac{\pi}{4}\right)\sec\left(\frac{\pi}{5}\right) \cdot \ \dots \]
M. MacLaurin et un peu de calcul différentiel
Une approche pour attaquer cette limite est de considérer son logarithme : \begin{align*}\ln\left(R\right) &= \ln\left(\sec\left(\frac{\pi}{3}\right)\sec\left(\frac{\pi}{4}\right)\sec\left(\frac{\pi}{5}\right) \cdot \ \dots\right)\\ \\ &=\ln\left(\sec\left(\frac{\pi}{3}\right)\right)+\ln\left(\sec\left(\frac{\pi}{4}\right)\right)+\ln\left(\sec\left(\frac{\pi}{5}\right)\right) + \ \dots\end{align*}car le logarithme d’un produit est égal à la somme des logarithmes. Les termes de la somme sont tous de la forme \[\ln\left(\sec\left(x\right)\right)\]Notons que si \(x \to 0\), alors \(\sec\left(x\right) \to 1\) et \(\ln\left(\sec\left(x\right)\right) \to 0\). Ainsi, les termes de la séries tendent vers \(0\). On considère la fonction \[f(x) = \ln\left(\sec\left(x\right)\right)\]Pour les petites valeurs de \(x\), soit \(0<x\leq \frac{\pi}{3}\), on peut s’intéresser aux premiers termes de sa série de MacLaurin et ainsi trouver une approximation polynomiale adéquate. La série de MacLaurin de \(f(x)\) est une série de Taylor centrée en \(x = 0\). C’est \[f(x) = f(0) + \frac{f'(0)}{1!}x + \frac{f’\, \!'(0)}{2!}x^{2} + \frac{f^{(3)}(0)}{3!}x^{3} + \ \dots \ + \frac{f^{(n)}(0)}{n!}x^{n}\ + \ \dots \ \]On peut calculer le premier terme, \(f(0)\), immédiatement, \begin{align*}f(0) &= \ln\left(\sec\left(0\right)\right)\\ \\ &=\ln\left(1\right) \\ \\ &=0\end{align*}Bon. Allons voir du côté du deuxième terme. Quelle est la dérivée de \(f'(x)\) ? En se rappelant que \[\frac{\text{d}}{\text{d}x}\big(\ln\left(x\right)\big) = \frac{1}{x}\] et que \[\frac{\text{d}}{\text{d}x}\big(\sec\left(x\right)\big) = \tan\left(x\right)\sec\left(x\right)\quad ^{[1]}\] et en utilisant le théorème de dérivation des fonctions composées, \[\frac{\text{d}}{\text{d}x}\big(f\left(g\left(x\right)\right)\big) = f’\left(g(x)\right) \cdot g’\left(x\right)\]on obtient\begin{align*}\frac{\text{d}}{\text{d}x}\big(\ln\left(\sec\left(x\right)\right)\big) &= \frac{1}{\sec\left(x\right)}\cdot \tan\left(x\right)\sec\left(x\right) \\ \\ &= \tan\left(x\right)\end{align*}On calcule\begin{align*}f’\left(0\right) &=\tan\left(0\right) \\ \\ &= 0\end{align*}Encore \(0\). Mince ! Intéressons-nous dans ce cas au prochain terme. Nous avons besoin de \(f’\, \!’\left(0\right)\). Puisque \[f’\left(x\right) = \tan\left(x\right)\] et que la dérivée de \(\tan\left(x\right)\) est \(\sec^{2}\left(x\right)\) [2], on obtient directement \[f’\, \!’\left(x\right) = \sec^{2}\left(x\right)\]On calcule \begin{align*}f’\, \!’\left(0\right) &= \sec^{2}\left(0\right) \\ \\ &= 1^{2} \\ \\ &=1\end{align*}Génial ! On sait donc que \begin{align*}f\left(x\right) &\approx f\left(0\right) + \frac{f’\left(0\right)}{1!}x + \frac{f’\, \!’\left(0\right)}{2!}x^{2} \\ \\ \ln\left(\sec\left(x\right)\right)&\approx0 + \frac{0}{1}x + \frac{1}{2}x^{2}\\ \\ &\approx\frac{1}{2}x^{2}\end{align*}
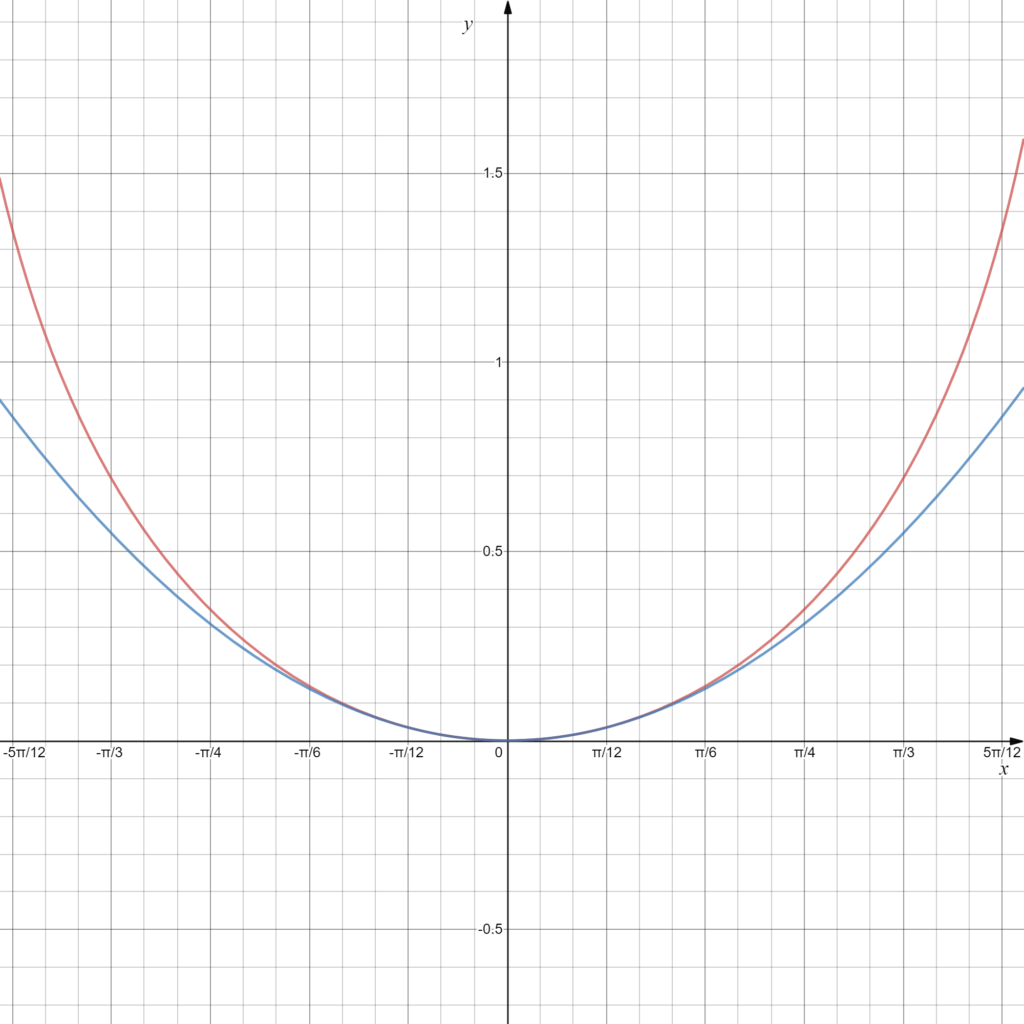
En rouge, \(\color{Red}{y=\ln\left(\sec\left(x\right)\right)}\), en bleu, \(\color{Blue}{y=\dfrac{1}{2}x^{2}}\)
On remarque que d’une part, pour les valeurs de \(x\) concernées, l’approximation semble adéquate et, d’autre part, qu’elle sous-estime la valeur (ce qu’on peut vérifier avec différentes valeurs de \(n\)). L’erreur est plus grande pour les premiers termes.
Cela étant dit, on obtient \begin{align*}\ln\left(R\right) &= \ln\left(\sec\left(\frac{\pi}{3}\right)\right)+\ln\left(\sec\left(\frac{\pi}{4}\right)\right)+\ln\left(\sec\left(\frac{\pi}{5}\right)\right) + \ \dots \\ \\ &\approx \frac{1}{2}\left(\frac{\pi}{3}\right)^{2} + \frac{1}{2}\left(\frac{\pi}{4}\right)^{2} + \frac{1}{2}\left(\frac{\pi}{6}\right)^{2} \ + \ \dots \\ \\ &\approx \frac{1}{2}\left(\frac{\pi^{2}}{9}\right) + \frac{1}{2}\left(\frac{\pi^{2}}{16}\right) + \frac{1}{2}\left(\frac{\pi^{2}}{25}\right)\ + \ \dots \\ \\ &\approx \frac{1}{2}\pi^{2}\left(\frac{1}{9} + \frac{1}{16} + \frac{1}{25}\ + \ \dots\ \right) \end{align*}La série converge car les termes dans la parenthèse correspondent à la série du problème de Bâle (moins les premiers termes) ! Sachant que \[1 + \frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \frac{1}{25} + \ \dots \ = \frac{\pi^{2}}{6}\]on peut utiliser ce résultat pour trouver une valeur approximative de \(\ln\left(R\right)\).\begin{align*}\ln\left(R\right)&\approx \frac{1}{2}\pi^{2}\left(\frac{1}{9} + \frac{1}{16} + \frac{1}{25}\ + \ \dots\ \right) \\ \\ &\approx \frac{1}{2}\pi^{2}\left(\frac{\pi^{2}}{6}-1-\frac{1}{4}\right) \\ \\ &\approx 1,\!95\end{align*}Cela implique que \begin{align*}R &\approx e^{1,95} \\ \\ &\approx7,\!03\end{align*}Grâce à l’ordinateur, on peut calculer une approximation numérique bien meilleure.
| Nombre de termes | \(R_n \approx\) | Approximation polynomiale |
|---|---|---|
| \(10\) | \(5,\!855363\) | \(4,\!731997\) |
| \(100\) | \(8,\!291083\) | \(6,\!691094\) |
| \(1\,000\) | \(8,\!657315\) | \(6,\!986634\) |
| \(10\,000\) | \(8,\!695745\) | \(7,\!017648\) |
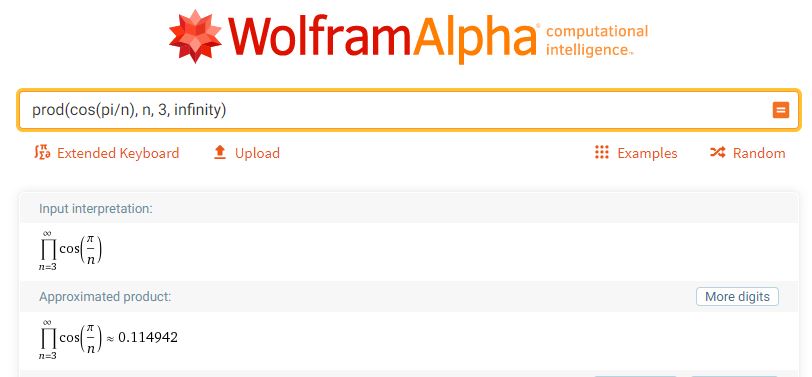
Notre approximation polynomiale s’avère finalement un peu décevante. Mais la route pour l’obtenir en a valu la peine ! Ce n’est pas la destination qui compte, c’est le voyage. On voit que la limite semble tendre vers une valeur près de \(8,\!7\), ce que confirme WolframAlpha.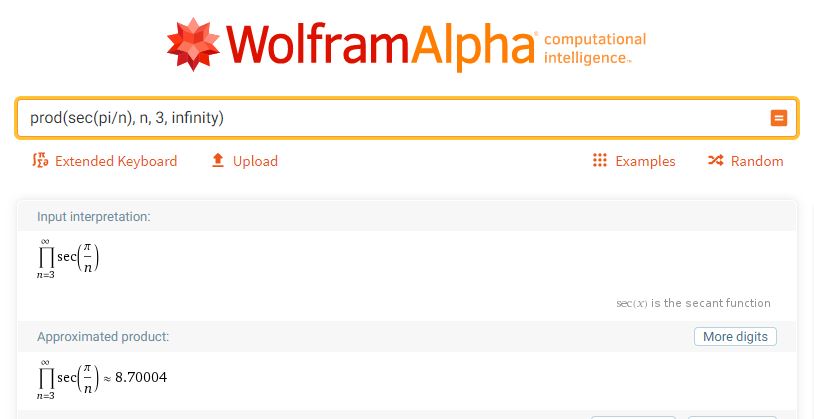
Ici, le cercle limite de rayon \(\approx 8, 7\) en bleu :
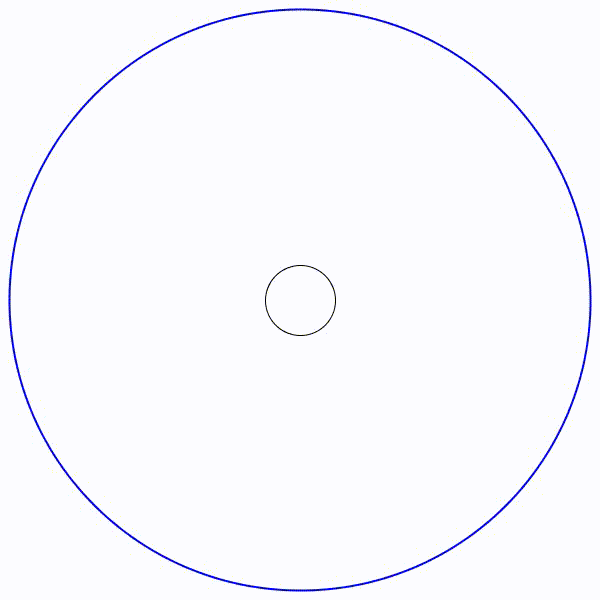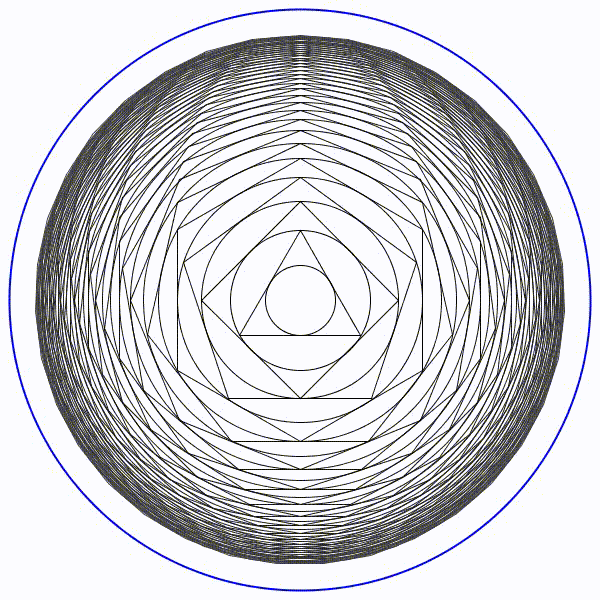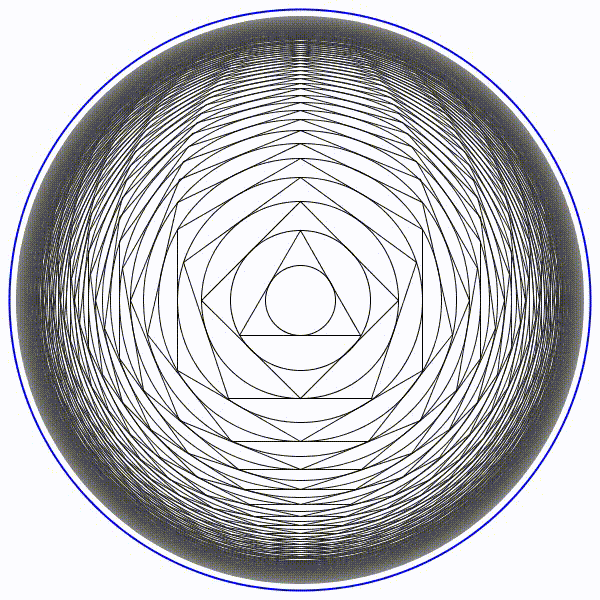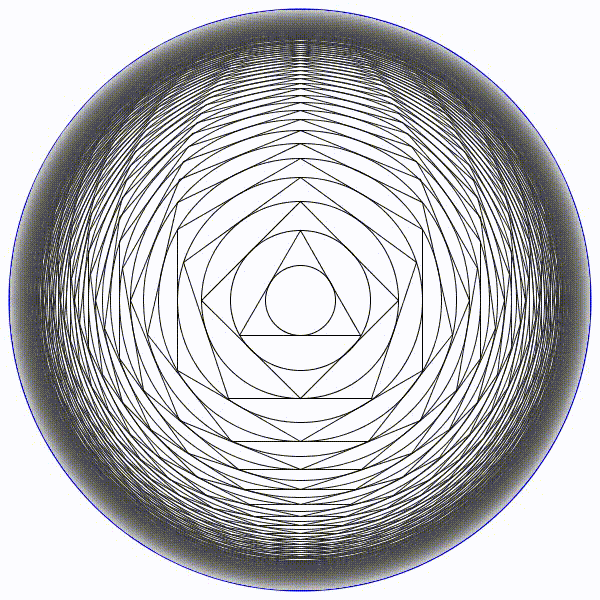
Le deuxième problème
Le deuxième problème se résout de manière analogue.

Puisque \[\cos\left(\frac{\theta}{2}\right) = \frac{r}{R}\]on a \[r=R\cos\left(\frac{\theta}{2}\right)\]De la même manière \[r = R\cos\left(\frac{\pi}{n}\right)\]
Puisque le rayon du cercle de départ est \(1\), on devra trouver la valeur de \[r = \cos\left(\frac{\pi}{3}\right)\cos\left(\frac{\pi}{4}\right)\cos\left(\frac{\pi}{5}\right)\ \cdot \ \dots\]
À l’instar de ce qu’on a fait précédemment, on cherche \[\ln\left(r\right) = \ln\left(\cos\left(\frac{\pi}{3}\right)\right) + \ln\left(\cos\left(\frac{\pi}{4}\right)\right) + \ln\left(\left(\frac{\pi}{5}\right)\right) \ + \ \dots \]Puisque cette fois-ci \[\ln\left(\cos\left(x\right)\right) \approx -\frac{x^{2}}{2}\]on obtient \begin{align*}\ln\left(r\right) &\approx -\frac{1}{2}\left(\frac{\pi}{3}\right)^{2} -\frac{1}{2}\left(\frac{\pi}{4}\right)^{2} -\frac{1}{2}\left(\frac{\pi}{5}\right)^{2} \ + \ \dots \\ \\ &\approx -\frac{1}{2}\pi^{2}\left(\frac{1}{9} + \frac{1}{16} + \frac{1}{25} + \ \dots \ \right) \\ \\ &\approx -1,\!95\end{align*}ce qui fait \begin{align*}r &\approx e^{-1,95} \\ \\ &\approx 0,\!14\end{align*}
L’approximation est-elle meilleure cette fois-ci ?
| Nombre de termes | \(r_n \approx\) | Approximation polynomiale |
|---|---|---|
| \(10\) | \(0,\!170783\) | \(0,\!211327\) |
| \(100\) | \(0,\!120611\) | \( 0,\!149452\) |
| \(1\,000\) | \(0,\!115509\) | \(0,\!143130\) |
| \(10\,000\) | \(0,\!114998\) | \(0,\!142497\) |
\(r\) semble tendre cette fois-ci vers environ \(0,\!115\). La même remarque s’applique.
À nouveau, l’animation avec le cercle limite de rayon \(\approx 0,\!115\) en bleu :
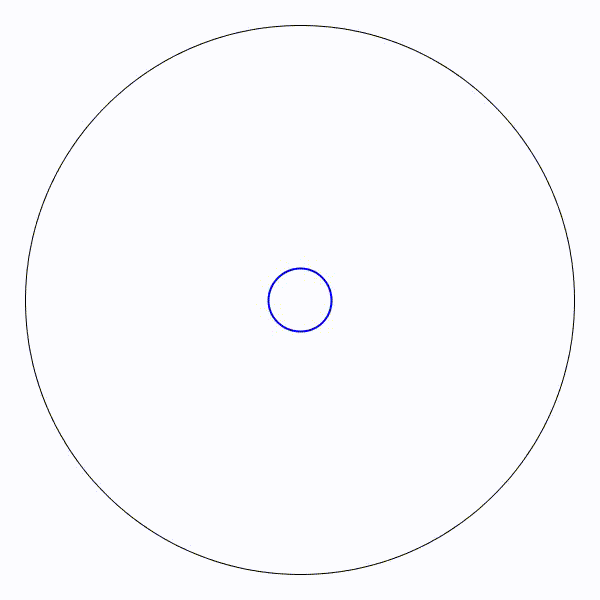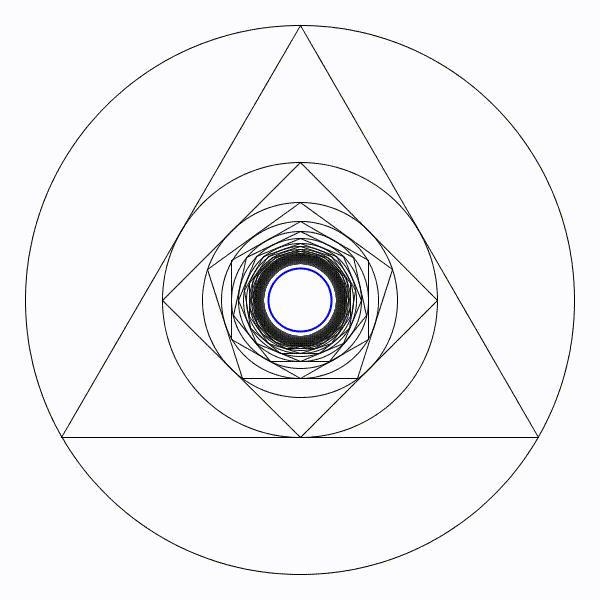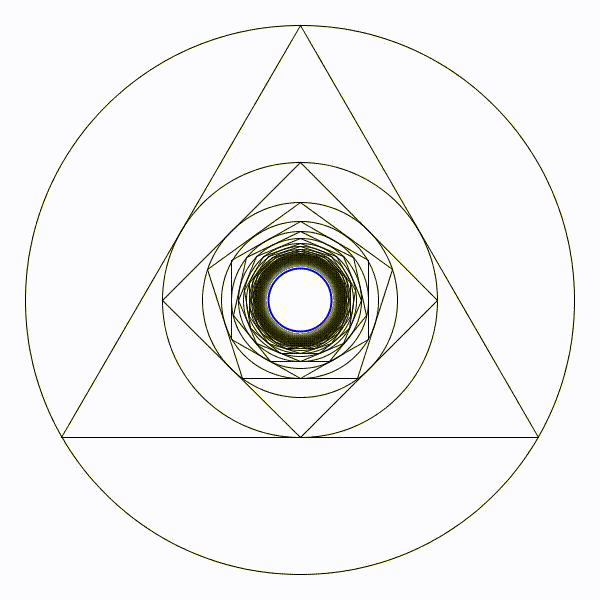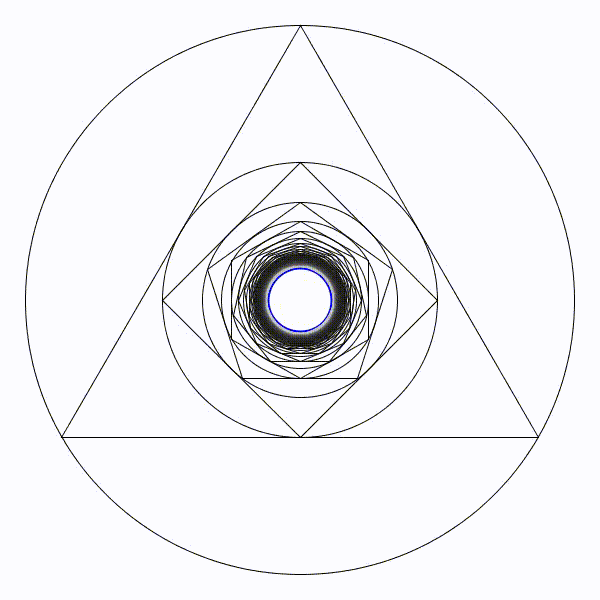
[0] Edward Kasner & James Newman, Mathematics and the Imagination, Dover, 2001 (Originalement Simon & Schuster, 1940)
[1] En utilisant la dérivée d’un quotient, \[\frac{\text{d}}{\text{d}x}\left(\frac{f\left(x\right)}{g\left(x\right)}\right) = \frac{f’\left(x\right)g\left(x\right)-f\left(x\right)g’\left(x\right)}{g^{2}\left(x\right)}\]et la dérivée de \(\cos\left(x\right)\) \[\frac{\text{d}}{\text{d}x}\big(\cos(x)\big) = -\sin\left(x\right)\]on obtient \begin{align*} \frac{\text{d}}{\text{d}x} \big(\sec\left(x\right)\big)&= \frac{\text{d}}{\text{d}x}\left(\frac{1}{\cos\left(x\right)}\right) \\ \\ &=\frac{0\cdot \left(\cos\left(x\right)\right)- 1\cdot \left(-\sin\left(x\right)\right)}{\cos^{2}\left(x\right)} \\ \\ &= \frac{0 + \sin\left(x\right)}{\cos^{2}\left(x\right)} \\ \\ &= \frac{\sin\left(x\right)}{\cos^{2}\left(x\right)}\\ \\ &= \frac{\sin\left(x\right)}{\cos\left(x\right)}\cdot \frac{1}{\cos\left(x\right)} \\ \\ &= \tan\left(x\right) \sec\left(x\right)\end{align*}
[2] Avec les mêmes outils qu’en [1] et en plus \[\frac{\text{d}}{\text{d}x}\big(\sin\left(x\right)\big) = \cos\left(x\right)\]et l’identitée trigonométrique fondamentale \[\sin^{2}\left(x\right) + \cos^{2}\left(x\right)= 1\]on obtient \begin{align*}\frac{\text{d}}{\text{d}x}\big(\tan\left(x\right)\big) &= \frac{\text{d}}{\text{d}x}\left(\frac{\sin\left(x\right)}{\cos\left(x\right)}\right) \\ \\ &= \frac{\cos\left(x\right)\cos\left(x\right)-\sin\left(x\right)\left(-\sin\left(x\right)\right)}{\cos^{2}\left(x\right)} \\ \\ &= \frac{\cos^2\left(x\right) + \sin^{2}\left(x\right)}{\cos^{2}\left(x\right)} \\ \\ &= \frac{1}{\cos^{2}\left(x\right)} \\ \\ &= \sec^{2}\left(x\right)\end{align*}
(9/12/2021) : Je viens de tomber par hasard sur ceci : le rayon du cercle limite intérieur (environ 0,11) est une constante baptisée ! C’est la constante de Kepler-Bouwkamp. L’autre rayon (environ 8,7) se trouve au bas de cette page.
Bonjour Dude,
J’ai découvert votre site il y a quelques temps déjà (avec le problème “Combien de triangles…”). En y revenant récemment je vois que vous aves résolu le problème des polygones emboîtés tiré du livre de Kasner & Newman “Les mathématiques et l’imagination” édité en 1970. Votre solution du calcul des limites dans les deux cas – polygones circonscrits et polygones inscrits – m’a vivement intéressé car je l’avais vainement cherchée dans les années 80. En effet, j’ai eu le bonheur d’écrire le livre “Graphisme dans le plan et dans l’espace avec Turbo Pascal 4.0” édité chez Masson, ouvrage dans lequel l’ordinateur dessinait les diverses enveloppes. J’avais écrit les deux formules permettant de calculer les rayons successifs et appelai à l’aide pour une preuve rigoureuse. Je n’ai jamais eu de réponse et ai dû attendre de la lire sur votre site. J’en suis très heureux et vous remercie.
Bien à vous
Robert DONY
Bonjour Robert,
merci du commentaire ! Comme vous le constatez, le site n’est pas totalement à l’abandon… mais le temps me manque !
Les animations ont été produites dans un langage basé sur la plate-forme Java, Processing. Les images statiques ont été réalisées avec Géogébra.
Au plaisir !
Bonjour,
Je suis tombé sur votre site en cherchant les relations qui existaient entre le cercle et le triangle. Depuis avoir vu vos modélisations et vos calculs (moi qui suis néophyte et incapable de reproduire ce genre de chose), je me pose cette question : quelle implication pratique cette découverte a t’elle eu ? y a til un impact sur les recherches scientifiques type astronomie ou autre ? Je suis surpris de voir que notre esprit se trompe à ce point car en effet on s’attend naturellement à aller sur l’infini ou le 0, or il n’en est rien…et ce n’est pas rien !
Merci de votre réponse.
Corentin
Bonjour,
En effet ce n’est pas rien. Je ne connais pas d’application directe plus concrète de ce résultat. Cependant je trouve qu’il s’agit d’un exemple très évocateur : parfois, l’intuition nous joue des tours, et c’est cette rigueur un peu austère qui vient nous éclairer.
Au plaisir !